Bài 5.7 trang 141 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Bài 5.7 trang 141 SGK Toán 11 tập 1 - Cùng khám phá
Bài 5.7 thuộc chương trình Toán 11 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
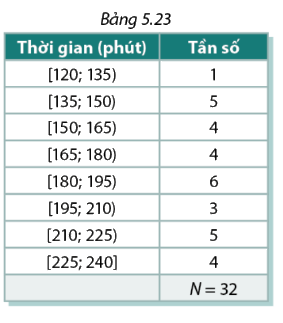
Bảng 5.23 biểu diễn kết quả thống kê về thời gian cần thiết để thực hiện cuộc chạy marathon đã được tổ chức ở một địa phương .
Đề bài
Bảng 5.23 biểu diễn kết quả thống kê về thời gian cần thiết để thực hiện cuộc chạy marathon đã được tổ chức ở một địa phương .
a, Xác định các tứ phân vị của mẫu số liệu
b, Xét nhóm gồm 50 % số cuộc thi có thời gian ngắn hơn đã được tổ chức. Thời gian tối đa của các cuộc thi trong nhóm này là bao nhiêu?

Phương pháp giải - Xem chi tiết
a, Sử dụng công thức tính các tứ phân vị
b, Thời gian tối đa của các cuộc thi trong nhóm này là \({Q_1}\)
Lời giải chi tiết
a, Bảng tần số tích lũy mẫu số liệu
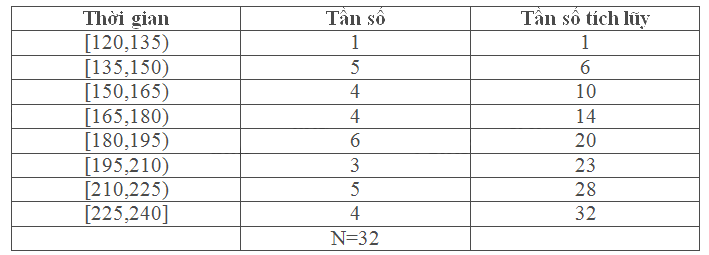
Ta có: \(\frac{N}{4} = \frac{{32}}{4} = 8 \Rightarrow \frac{N}{2} = 16 \Rightarrow \frac{{3N}}{4} = 24\)
Các nhóm chứa \({Q_1}\), \({Q_2}\) và \({Q_3}\) là [150,165), [180,195) và [210,225)
Độ dài các nhóm ghép đều là h=15
Ta có: \({L_1} = 150,{n_1} = 4,{T_1} = 6\)\( \Rightarrow {Q_1} = {L_1} + \frac{{\frac{N}{4} - {T_1}}}{{{n_1}}}.h = 150 + \frac{{8 - 6}}{4}.15 = 157,5\)
\({L_2} = 180,{n_2} = 6,{T_2} = 14\)\( \Rightarrow {Q_2} = {L_2} + \frac{{\frac{N}{2} - {T_2}}}{{{n_2}}}.h = 180 + \frac{{16 - 14}}{6}.15 = 185\)
\({L_3} = 210,{n_3} = 5,{T_3} = 23\)\( \Rightarrow {Q_3} = {L_3} + \frac{{\frac{{3N}}{4} - {T_3}}}{{{n_3}}}.h = 210 + \frac{{24 - 23}}{5}.15 = 213\)
b, Thời gian tối đa của các cuộc thi trong nhóm này là \({Q_1}\)=157,5 phút .
Bài 5.7 trang 141 SGK Toán 11 tập 1 - Cùng khám phá: Giải chi tiết và hướng dẫn
Bài 5.7 trang 141 SGK Toán 11 tập 1 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tối ưu hóa một đại lượng nào đó bằng cách sử dụng đạo hàm. Để giải bài toán này, chúng ta cần thực hiện các bước sau:
- Xác định hàm số: Đầu tiên, cần xác định hàm số biểu diễn đại lượng cần tối ưu hóa. Hàm số này thường phụ thuộc vào một hoặc nhiều biến số.
- Tìm tập xác định của hàm số: Xác định miền giá trị của các biến số trong hàm số.
- Tính đạo hàm: Tính đạo hàm bậc nhất của hàm số.
- Tìm điểm dừng: Giải phương trình đạo hàm bằng 0 để tìm các điểm dừng của hàm số.
- Xác định cực trị: Sử dụng đạo hàm bậc hai hoặc phương pháp xét dấu đạo hàm bậc nhất để xác định các điểm cực trị của hàm số.
- Tìm giá trị lớn nhất/nhỏ nhất: So sánh các giá trị của hàm số tại các điểm cực trị và tại các điểm biên của tập xác định để tìm giá trị lớn nhất và nhỏ nhất của hàm số.
Ví dụ minh họa
Giả sử bài toán yêu cầu tìm kích thước của một hình chữ nhật có diện tích cố định sao cho chu vi nhỏ nhất. Ta có thể giải bài toán này như sau:
- Gọi chiều dài và chiều rộng của hình chữ nhật là x và y.
- Diện tích của hình chữ nhật là xy = S (S là hằng số).
- Chu vi của hình chữ nhật là P = 2(x + y).
- Từ xy = S, ta có y = S/x.
- Thay vào công thức tính chu vi, ta được P = 2(x + S/x).
- Tính đạo hàm của P theo x: P' = 2(1 - S/x2).
- Giải phương trình P' = 0, ta được x = √S.
- Khi đó, y = S/√S = √S.
- Vậy, hình chữ nhật có chu vi nhỏ nhất là hình vuông có cạnh bằng √S.
Lưu ý quan trọng
Khi giải các bài toán tối ưu hóa bằng đạo hàm, cần chú ý các điểm sau:
- Kiểm tra xem hàm số có đạt cực trị tại các điểm dừng hay không.
- Xem xét các điểm biên của tập xác định.
- Đảm bảo rằng các giá trị tìm được có ý nghĩa trong thực tế.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự trong SGK Toán 11 tập 1 và các tài liệu tham khảo khác. tusach.vn cung cấp đầy đủ các bài giải chi tiết và hướng dẫn giải các bài tập Toán 11 tập 1, giúp bạn học tập hiệu quả hơn.
Kết luận
Bài 5.7 trang 141 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng đạo hàm để giải quyết các bài toán thực tế. Việc nắm vững các bước giải và các lưu ý quan trọng sẽ giúp bạn tự tin giải quyết các bài toán tương tự.