Giải mục 4 trang 62 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 4 trang 62 SGK Toán 11 tập 2 - Cùng khám phá
Chào mừng bạn đến với lời giải chi tiết mục 4 trang 62 SGK Toán 11 tập 2 trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Bài viết này sẽ cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải chi tiết, giúp bạn tự tin hơn trong quá trình học tập môn Toán 11.
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot \left( {ABCD} \right)\).
Hoạt động 6
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot \left( {ABCD} \right)\).
a) Tìm hình chiếu \(d\) của \(A'C\) trên mặt phẳng \(\left( {ABCD} \right)\). Xác định góc giữa \(A'C\) và \(d\)
b) Tìm hình chiếu \(a\) của \(A'C'\) trên mặt phẳng \(\left( {ABCD} \right)\). Xác định góc giữa \(A'C'\) và \(a\)
Phương pháp giải:
a) Chứng minh \(A'A \bot \left( {ABCD} \right)\) từ đó suy ra \(A'\) là hình chiếu của \(A\) trên \(\left( {ABCD} \right)\)
b) Chứng minh \(CC' \bot \left( {ABCD} \right)\) từ đó suy ra \(C'\) là hình chiếu của \(C\) trên \(\left( {ABCD} \right)\)
Lời giải chi tiết:
a) Vì \(A'A \bot \left( {ABCD} \right)\) nên \(A\) là hình chiếu của \(A'\) trên \(\left( {ABCD} \right)\)
Vậy hình chiếu \(d\) của \(A'C\) trên \(\left( {ABCD} \right)\) là \(AC\)
Góc giữa \(A'C\) và \(AC\) là góc \(\widehat {A'CA}\)
b) Vì \(A'A \bot \left( {ABCD} \right)\) nên \(A\) là hình chiếu của \(A'\) trên \(\left( {ABCD} \right)\)
Vì \(CC' \bot \left( {ABCD} \right)\) nên \(C\) là hình chiếu của \(C'\) trên \(\left( {ABCD} \right)\)
Vậy hình chiếu \(a\) của \(A'C'\) trên \(\left( {ABCD} \right)\) là \(AC\)
Vì \(A'C'//AC\) nên góc giữa \(A'C'\) và \(AC\) bằng \({0^o}\)
Luyện tập 8
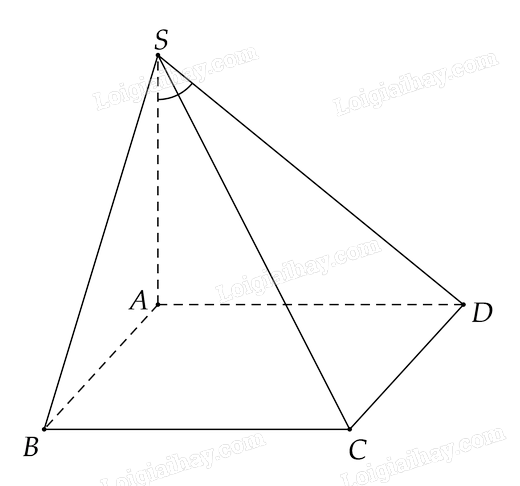
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\), \(SA = a\sqrt 3 \). Xác định và tính góc giữa đường thẳng \(SD\) và \(\left( {SAB} \right)\)
Phương pháp giải:
Xác định giao điểm \(S\) của \(SD\) và \(\left( {SAB} \right)\)
Chứng minh \(DA \bot \left( {SAB} \right)\) từ đó suy ra \(SA\) là hình chiếu vuông góc của \(SD\) trên \(\left( {SAB} \right)\) suy ra góc cần tìm là góc giữa 2 đường thẳng \(SD\) và \(SA\)
Sử dụng tỉ số lượng giác trong tam giác vuông
Lời giải chi tiết:

Ta có \(S\) là giao điểm của \(SD\) và \(\left( {SAB} \right)\) \(\left( 1 \right)\)
Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AD\).
Vì \(ABCD\) là hình vuông lên \(AD \bot AB\)
Ta có \(\left\{ \begin{array}{l}AD \bot SA\\AD \bot AB\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right) \Rightarrow \)\(A\) là hình chiếu vuông góc của \(D\) trên \(\left( {SAB} \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(SA\) là hình chiếu vuông góc của \(SD\) trên \(\left( {SAB} \right)\)
Vậy góc giữa \(SD\) và \(\left( {SAB} \right)\) là góc giữa \(SA\) và \(SD\) là góc giữa \(\widehat {DSA}\)
Xét \(\Delta SAD\) vuông tại \(A\) có \(\tan S = \frac{{AD}}{{SA}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {ASD} = {30^o}\)
Giải mục 4 trang 62 SGK Toán 11 tập 2: Tổng quan và Phương pháp tiếp cận
Mục 4 trang 62 SGK Toán 11 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các dạng bài tập tính đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, và giải các bài toán liên quan đến đạo hàm. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về định nghĩa đạo hàm, các quy tắc tính đạo hàm, và các ứng dụng của đạo hàm.
Nội dung chi tiết Giải mục 4 trang 62 SGK Toán 11 tập 2
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 4 trang 62 SGK Toán 11 tập 2, chúng ta sẽ đi vào phân tích từng bài tập cụ thể:
Bài 1: Tính đạo hàm của hàm số
Bài tập này yêu cầu học sinh vận dụng các quy tắc tính đạo hàm cơ bản để tìm đạo hàm của các hàm số đơn giản. Ví dụ:
- Hàm số đa thức: Sử dụng quy tắc đạo hàm của tổng, hiệu, tích, thương và quy tắc lũy thừa.
- Hàm số lượng giác: Sử dụng các công thức đạo hàm của sinx, cosx, tanx, cotx.
- Hàm số mũ và logarit: Sử dụng các công thức đạo hàm của ex, ax, logax.
Bài 2: Ứng dụng đạo hàm để khảo sát hàm số
Bài tập này yêu cầu học sinh sử dụng đạo hàm để xác định các khoảng đơn điệu, cực trị, và điểm uốn của hàm số. Các bước thực hiện như sau:
- Tính đạo hàm cấp nhất: y' = f'(x)
- Tìm điểm dừng: Giải phương trình f'(x) = 0
- Xác định dấu của đạo hàm cấp nhất: Xét dấu f'(x) trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến.
- Tính đạo hàm cấp hai: y'' = f''(x)
- Tìm điểm uốn: Giải phương trình f''(x) = 0
- Xác định dấu của đạo hàm cấp hai: Xét dấu f''(x) trên các khoảng xác định để xác định điểm uốn.
Bài 3: Giải các bài toán liên quan đến đạo hàm
Bài tập này có thể bao gồm các bài toán về tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc các bài toán ứng dụng đạo hàm trong thực tế. Để giải quyết các bài toán này, học sinh cần kết hợp kiến thức về đạo hàm với các kiến thức khác trong chương trình Toán 11.
Lưu ý khi giải bài tập mục 4 trang 62 SGK Toán 11 tập 2
Để đạt được kết quả tốt nhất khi giải bài tập mục 4 trang 62 SGK Toán 11 tập 2, học sinh cần lưu ý những điều sau:
- Nắm vững các định nghĩa và quy tắc: Đảm bảo bạn hiểu rõ các khái niệm và công thức liên quan đến đạo hàm.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
- Sử dụng tài liệu tham khảo: Tham khảo thêm các tài liệu tham khảo khác để hiểu rõ hơn về nội dung bài học.
Kết luận
Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn trong quá trình học tập môn Toán 11. Chúc các em học tốt và đạt kết quả cao!
| Bài tập | Nội dung chính | Phương pháp giải |
|---|---|---|
| Bài 1 | Tính đạo hàm | Áp dụng quy tắc tính đạo hàm |
| Bài 2 | Khảo sát hàm số | Sử dụng đạo hàm cấp 1 và cấp 2 |
| Bài 3 | Ứng dụng đạo hàm | Kết hợp kiến thức về đạo hàm và các kiến thức khác |