Bài 7.24 Trang 50 SGK Toán 11 Tập 2

Bài 7.24 trang 50 SGK Toán 11 tập 2 - Cùng khám phá

Bài 7.24 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các công thức đạo hàm cơ bản và kỹ năng giải quyết bài toán liên quan đến ứng dụng của đạo hàm.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho hàm số \(f\left( x \right)\) có đồ thị là đường cong \(\left( C \right)\) tròn Hình 7.11

Đề bài

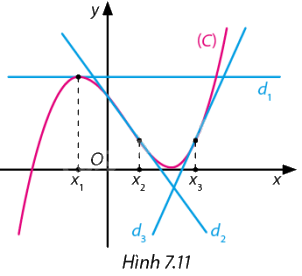
Cho hàm số \(f\left( x \right)\) có đồ thị là đường cong \(\left( C \right)\) tròn Hình 7.11. Biết \({d_1},{d_2},{d_3}\) là các tiếp tuyến của \(\left( C \right)\) tại các điểm có hoành độ là \({x_1};{x_2}\) và \({x_3}\). Khẳng định nào dưới đây đúng?

Bài 7.24 trang 50 SGK Toán 11 tập 2 - Cùng khám phá 1

A. \(f'\left( {{x_3}} \right) < f'\left( {{x_2}} \right) < f'\left( {{x_1}} \right).\)

B. \(f'\left( {{x_3}} \right) < f'\left( {{x_1}} \right) < f'\left( {{x_2}} \right).\)

C. \(f'\left( {{x_2}} \right) < f'\left( {{x_1}} \right) < f'\left( {{x_3}} \right).\)

D. \(f'\left( {{x_1}} \right) < f'\left( {{x_2}} \right) < f'\left( {{x_3}} \right).\)

Phương pháp giải - Xem chi tiết Bài 7.24 trang 50 SGK Toán 11 tập 2 - Cùng khám phá 2

Dựa vào hệ số góc của tiếp tuyến là \(f'\left( x \right)\)

Dựa vào đặc điểm đồng biến, nghịch biến của ba dường thẳng \({d_1},{d_2},{d_3}\)

Lời giải chi tiết

Đáp án C

Ta có hệ số góc của tiếp tuyến là \(f'\left( x \right)\)

Vì \({d_1}//Ox\) nên hệ số góc của \({d_1}\) bằng 0. Do đó \(f'\left( {{x_1}} \right) = 0\)

Vì \({d_2}\) nghịch biến nên hệ số góc của \({d_2}\) là \(f'\left( {{x_2}} \right) < 0\)

Vì \({d_3}\) đồng biến nên hệ số góc của \({d_3}\) là \(f'\left( {{x_3}} \right) > 0\)

Do đó \(f'\left( {{x_2}} \right) < f'\left( {{x_1}} \right) < f'\left( {{x_3}} \right).\)

Bài 7.24 Trang 50 SGK Toán 11 Tập 2: Giải Chi Tiết và Phân Tích

Bài 7.24 trang 50 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Bài tập này thường liên quan đến việc tìm đạo hàm của hàm số, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến, và tìm cực trị của hàm số.

Nội dung bài tập 7.24

Thông thường, bài 7.24 sẽ đưa ra một hàm số cụ thể và yêu cầu học sinh thực hiện các thao tác sau:

Tính đạo hàm của hàm số.
Tìm tập xác định của hàm số.
Xác định các điểm làm đạo hàm bằng 0 hoặc không xác định.
Lập bảng biến thiên của hàm số.
Kết luận về khoảng đồng biến, nghịch biến, cực đại, cực tiểu của hàm số.

Phương pháp giải bài tập 7.24

Để giải bài tập 7.24 một cách hiệu quả, học sinh cần:

Nắm vững các công thức đạo hàm cơ bản: Đạo hàm của các hàm số đơn giản như xⁿ, sinx, cosx, tanx, e^x, ln(x),...
Sử dụng các quy tắc đạo hàm: Quy tắc cộng, trừ, nhân, chia, quy tắc hàm hợp,...
Phân tích bài toán: Xác định rõ yêu cầu của bài toán và lựa chọn phương pháp giải phù hợp.
Kiểm tra lại kết quả: Đảm bảo rằng kết quả tính toán là chính xác và phù hợp với điều kiện của bài toán.

Ví dụ minh họa (giả định một dạng bài tập phổ biến)

Bài tập: Tìm cực trị của hàm số y = x³ - 3x² + 2.

Giải:

Tính đạo hàm: y' = 3x² - 6x
Tìm điểm làm đạo hàm bằng 0: 3x² - 6x = 0 => x = 0 hoặc x = 2
Lập bảng biến thiên:
x -∞ 0 2 +∞
y' + - +
y ↗ ↘ ↗
Kết luận: Hàm số đạt cực đại tại x = 0, y_max = 2 và đạt cực tiểu tại x = 2, y_min = -2.

x	-∞	0	2	+∞
y'	+	-	+
y	↗	↘	↗

Lưu ý quan trọng

Khi giải bài tập về đạo hàm, cần chú ý đến tập xác định của hàm số và các điểm không xác định của đạo hàm. Việc lập bảng biến thiên là một công cụ hữu ích để xác định khoảng đồng biến, nghịch biến, cực đại, cực tiểu của hàm số.

Tusach.vn – Hỗ trợ học tập Toán 11 hiệu quả

tusach.vn cung cấp đầy đủ các bài giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 2. Ngoài ra, chúng tôi còn cung cấp các bài giảng video, bài tập trắc nghiệm và các tài liệu học tập khác để giúp học sinh học tập Toán 11 một cách hiệu quả nhất. Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm!