Giải mục 2 trang 85, 86, 87, 88, 89, 90 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 85, 86, 87, 88, 89, 90 SGK Toán 11 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 85, 86, 87, 88, 89, 90 sách giáo khoa Toán 11 tập 1.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
Trong hình học phẳng, qua hai điểm phân biệt có thể xác định được bao nhiêu đường thẳng?
Hoạt động 2
Trong hình học phẳng, qua hai điểm phân biệt có thể xác định được bao nhiêu đường thẳng?
Phương pháp giải:
Trong hình học phẳng, qua hai điểm phân biệt chỉ có thể xác định một đường thẳng.
Lời giải chi tiết:
Trong hình học phẳng, qua hai điểm phân biệt chỉ có thể xác định một đường thẳng.
Hoạt động 3
a) Hãy sử dụng một giấy bìa cứng, vẽ và cắt thành hình một tam giác đều ABC như Hình 4.15. Lấy các điểm M, N, P lần lượt là trung điểm của AB, BC, CA, sau đó gấp lại theo các đường nét đứt MN, NP, PM và dán các mép với nhau bằng băng dính để được mô hình có hình biểu diễn như Hình 4.16.
b) Sử dụng thêm một tấm bìa cứng phẳng (H), có thể đặt (H) chạm đồng thời vào bốn vị trí tương ứng với bốn điểm A, M, N, P hay không?
Phương pháp giải:
Gấp hình theo hướng dẫn của đề bài để quan sát.
Lời giải chi tiết:
Không thể đặt (H) chạm đồng thời vào bốn vị trí tương ứng với bốn điểm A, M, N, P.
Hoạt động 4
Vì sao người thợ xây thường dùng cây gỗ thẳng dài rê trên bề mặt sàn sau khi đổ bê tông? Vì sao người thợ mộc thường rê thước thẳng trên mặt bàn sau khi bào nhẵn mặt bàn (Hình 4.17)?

Phương pháp giải:
Quan sát thực tế.
Lời giải chi tiết:
Người thợ xây thường dùng cây gỗ thẳng dài rê trên bề mặt sàn sau khi đổ bê tông và người thợ mộc thường rê thước thẳng trên mặt bàn sau khi bào nhẵn mặt bàn để xem mặt sàn, mặt bàn đã nhẵn và phẳng chưa.
Luyện tập 3
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC, BD. Khi đó, O và D có thuộc mặt phẳng (ABC) không?
Phương pháp giải:
Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Lời giải chi tiết:

Ta thấy\(A,C \in \left( {ABC} \right)\). Mà \(O \in AC \Rightarrow O \in \left( {ABC} \right)\).
Lại thấy \(O,B \in \left( {ABC} \right)\). Mà \(D \in OB \Rightarrow D \in \left( {ABC} \right)\).
Hoạt động 5
a) Quan sát trong lớp học, xem mặt trường (có chứa bảng xanh) và sàn nhà là hình ảnh của hai mặt phẳng phân biệt (Hình 4.19). Hãy chỉ ra một số điểm chung của hai mặt phẳng này.
b) Đặt quyển sách thẳng đứng trên mặt bàn và mở ra thành hai nửa (Hình 4.20). Xem hai trang giấy trước mặt là hình ảnh của hai mặt phẳng phân biệt (P), (Q). Hãy chỉ ra ít nhất ba điểm vừa thuộc (P) vừa thuộc (Q) và nhận xét về vị trí của các điểm này.

Phương pháp giải:
Quan sát hình ảnh.
Lời giải chi tiết:
a) Các điểm chung của mặt tường và sàn nhà nằm trên đường chân tường.
b) Các điểm vừa thuộc (P) vừa thuộc (Q) đều nằm trên cùng 1 đường thẳng chung của (P) và (Q) là gáy sách.
Luyện tập 4
Bạn Nam cầm một miếng bìa hình tam giác với 3 đỉnh là A, B, C (Hình 4.23) đưa lên không quá cao so với mặt bàn và khẳng định rằng: “Nếu ta đặt các thanh thước dài dọc theo các cạnh AB, BC, CA để các thanh thước này chạm vào mặt bàn lần lượt tại các vị trí đánh dấu là điểm D, E, F thì ba điểm này thẳng hàng”. Bạn Mai không đồng ý và khẳng định: “D, E, F không thẳng hàng dược vì A, B, C không thẳng hàng”. Hãy cho biết ai đúng, ai sai? Vì sao?

Phương pháp giải:
Các điểm thuộc giao tuyến của 2 mặt phẳng phân biệt thì thẳng hàng.
Lời giải chi tiết:
Gọi mặt phẳng bàn là (Q).
Theo đầu bài thì \(D,E,F \in \left( {ABC} \right)\) và \(\left( Q \right)\).
Vậy ba điểm \(D,E,F\) cùng thuộc đường thẳng chung của \(\left( {ABC} \right)\) và \(\left( Q \right)\) nên \(D,E,F\) thẳng hàng.
Hoạt động 6
a) Cho ba điểm A, B, C không thẳng hàng, một đường thẳng d đi qua hai điểm B, C. Hãy xác định một mặt phẳng chứa cả điểm A và đường thẳng d.
b) Cho hai đường thẳng a, b cắt nhau tại điểm I. Trên các đường thẳng a, b lần lượt lấy các điểm A và B không trùng I. Các đường thẳng a, b có nằm trong mặt phẳng (ABI) hay không?
Phương pháp giải:
Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Lời giải chi tiết:
a)

b)
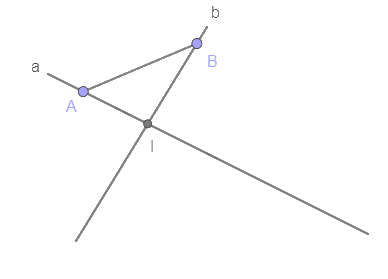
\(A,I \in \left( {ABI} \right) \Rightarrow \)Đường thẳng a cũng thuộc mặt phẳng (ABI).
\(B,I \in \left( {ABI} \right) \Rightarrow \) Đường thẳng b cũng thuộc mặt phẳng (ABI).
Luyện tập 5
Trong mặt phẳng (P), cho tam giác ABC. Lấy S là điểm không thuộc mặt phẳng (P). Có hay không một mặt phẳng chứa cả hai đường thẳng SA và BC?
Phương pháp giải:
Chứng minh phản chứng: Giả sử tồn tại một mặt phẳng chứa 2 đường thẳng SA và BC. Chứng minh S không thuộc mặt phẳng đó.
Lời giải chi tiết:

Giả sử có tồn tại mặt phẳng (Q) chứa 2 đường thẳng SA, BC. Khi đó S, A, B, C cùng thuộc mặt phẳng (Q). Ta có (Q) cũng chính là mặt phẳng (ABC). Suy ra S thuộc (ABC), mâu thuẫn với giả thiết S không thuộc (ABCD). Vậy không có mặt phẳng nào chứa cả hai đường thẳng SD và BC.
Vận dụng 1
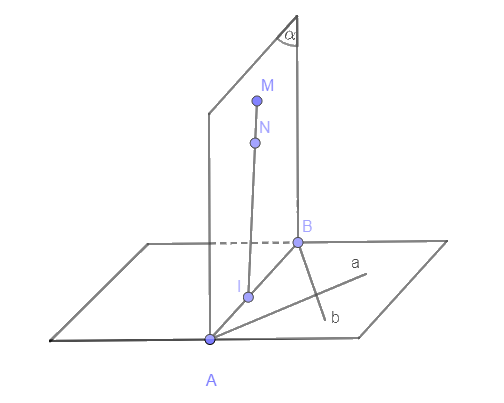
Cho hai đường thẳng a và b cắt nhau và hai điểm M, N không nằm trong mặt phẳng (a, b). Biết rằng đường thằng MN và mặt phẳng (a, b) luôn có một điểm chung. Một mặt phẳng \(\left( \alpha \right)\) thay đổi luôn luôn chứa MN và \(\left( \alpha \right)\) có điểm chung với hai đường thẳng a, b lần lượt là A, B. Chứng minh rằng dường thẳng AB luôn đi qua một điểm cố định khi \(\left( \alpha \right)\) thay đổi.
Phương pháp giải:
Nếu 2 mặt phẳng phân biệt có một điểm chung thì chúng có 1 đường thẳng chung duy nhất chứa tất cả các điểm chung của 2 mặt phẳng đó.
Chứng minh AB luôn đi qua điểm chung đó.
Lời giải chi tiết:

Gọi I là điểm chung của MN và mặt phẳng \(\left( {a,b} \right)\).
Mặt phẳng \(\left( \alpha \right)\) và hai đường thẳng a, b có điểm chung là A, B \( \Rightarrow \left( \alpha \right) \cap \left( {a,b} \right) = AB\)
Mà: \(MN \in \left( \alpha \right)\)
Nên \(I \in AB\)
Vì MN và \(\left( {a,b} \right)\) không thay đổi nên I không thay đổi.
Vậy đường thẳng AB luôn đi qua một điểm cố định khi \(\left( \alpha \right)\) thay đổi.
Giải mục 2 trang 85, 86, 87, 88, 89, 90 SGK Toán 11 tập 1 - Cùng khám phá
Mục 2 của SGK Toán 11 tập 1 thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững kiến thức và kỹ năng giải các bài tập trong mục này là vô cùng quan trọng, không chỉ để hoàn thành tốt bài kiểm tra trên lớp mà còn là nền tảng cho các kiến thức nâng cao hơn trong chương trình học.
Nội dung chính của mục 2
- Phép tịnh tiến: Tìm hiểu về định nghĩa, tính chất và cách thực hiện phép tịnh tiến trong mặt phẳng.
- Phép quay: Khám phá định nghĩa, tính chất và cách thực hiện phép quay quanh một điểm cho trước.
- Phép đối xứng trục: Nghiên cứu về định nghĩa, tính chất và cách thực hiện phép đối xứng qua một đường thẳng.
- Phép đối xứng tâm: Tìm hiểu về định nghĩa, tính chất và cách thực hiện phép đối xứng qua một điểm.
- Bài tập vận dụng: Giải các bài tập ứng dụng các phép biến hình để giải quyết các bài toán hình học.
Hướng dẫn giải chi tiết các bài tập trang 85, 86, 87, 88, 89, 90
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 2, trang 85, 86, 87, 88, 89, 90 SGK Toán 11 tập 1:
Bài 1 (Trang 85):
Bài này yêu cầu các em xác định ảnh của một điểm hoặc một hình qua phép tịnh tiến. Để giải bài này, các em cần nắm vững công thức của phép tịnh tiến: x' = x + a, y' = y + b, trong đó (a, b) là vectơ tịnh tiến.
Bài 2 (Trang 86):
Bài này yêu cầu các em xác định ảnh của một điểm hoặc một hình qua phép quay. Để giải bài này, các em cần nắm vững công thức của phép quay quanh gốc tọa độ O(0,0) với góc quay α: x' = xcosα - ysinα, y' = xsinα + ycosα.
Bài 3 (Trang 87):
Bài này yêu cầu các em xác định ảnh của một điểm hoặc một hình qua phép đối xứng trục. Để giải bài này, các em cần nắm vững tính chất của phép đối xứng trục: ảnh của một điểm M qua đường thẳng d là điểm M' sao cho d là đường trung trực của đoạn thẳng MM'.
Bài 4 (Trang 88):
Bài này yêu cầu các em xác định ảnh của một điểm hoặc một hình qua phép đối xứng tâm. Để giải bài này, các em cần nắm vững tính chất của phép đối xứng tâm: ảnh của một điểm M qua điểm I là điểm M' sao cho I là trung điểm của đoạn thẳng MM'.
Bài 5, 6, 7, 8, 9, 10 (Trang 89-90):
Các bài tập này thường là các bài tập vận dụng tổng hợp các kiến thức về các phép biến hình. Để giải các bài tập này, các em cần phân tích kỹ đề bài, xác định các phép biến hình cần thực hiện và áp dụng các công thức và tính chất đã học.
Lưu ý khi giải bài tập
- Đọc kỹ đề bài và xác định yêu cầu của bài toán.
- Vẽ hình minh họa để dễ dàng hình dung bài toán.
- Áp dụng đúng công thức và tính chất của các phép biến hình.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập trong mục 2 trang 85, 86, 87, 88, 89, 90 SGK Toán 11 tập 1. Chúc các em học tập tốt!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ nhé!