Giải mục 1 trang 14, 15 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 14, 15 SGK Toán 11 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 14, 15 SGK Toán 11 tập 2 tại tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho quá trình học tập của các em, tusach.vn đã biên soạn bộ giải bài tập Toán 11 tập 2 đầy đủ và chính xác.
Cho biểu thức \(y = {2^x}\), trong đó x là một số thực lấy giá trị tùy ý.
Hoạt động 1
Cho biểu thức \(y = {2^x}\), trong đó x là một số thực lấy giá trị tùy ý.
a) Hãy tính giá trị của y tương ứng với mỗi giá trị của x được cho trong bảng sau:
b) Với mỗi giá trị của x, ta tính được bao nhiêu giá trị của y? y có phải là hàm số của x không? Vì sao?
c) Biểu thức \(y = {\left( { - 3} \right)^x}\) có xác định một hàm số khi x lấy giá trị trong tập số thực \(\mathbb{R}\) không? Vì sao?
Phương pháp giải:
a) Thay x = 3; 0,5; \( - \frac{3}{7}\); \(\sqrt 2 \); \( - \sqrt 3 \) vào biểu thức \(y = {2^x}\).
b) Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
c) Khi số mũ nằm trong khoảng (0;1) thì cơ số không thể âm.
Lời giải chi tiết:
a)
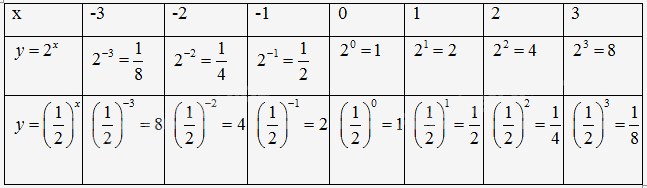
b) Với mỗi giá trị của x chỉ tính được một giá trị của y. y là hàm số của x vì mỗi một giá trị của x thì ta luôn xác định được chỉ một giá trị tương ứng của y.
c) Biểu thức \(y = {\left( { - 3} \right)^x}\) không xác định một hàm số khi x lấy giá trị trong tập số thực \(\mathbb{R}\). Vì khi \(x = \frac{1}{2}\), ta có: \({\left( { - 3} \right)^{\frac{1}{2}}} = \sqrt { - 3} \) (Vô lí)
Luyện tập 1
Trong các hàm số sau, hàm số nào là hàm số mũ, với cơ số bao nhiêu? Vì sao?
a) \(y = {3^{2x}}\)
b) \(y = {\left( { - \pi } \right)^x}\)
c) \(y = {x^{ - 4}}\)
d) \(y = {4^{ - x}}\)
Phương pháp giải:
Hàm số \(y = {a^x}\) được gọi là hàm số mũ cơ số a với a là một số thực dương khác 1.
Lời giải chi tiết:
a) \(y = {3^{2x}}\) là hàm số mũ với cơ số bằng 3.
b) \(y = {\left( { - \pi } \right)^x}\) là hàm số mũ với cơ số bằng \(\pi \).
c) \(y = {x^{ - 4}}\) không là hàm số mũ vì cơ số không phải hằng số.
d) \(y = {4^{ - x}}\) là hàm số mũ với cơ số bằng 4.
Hoạt động 2
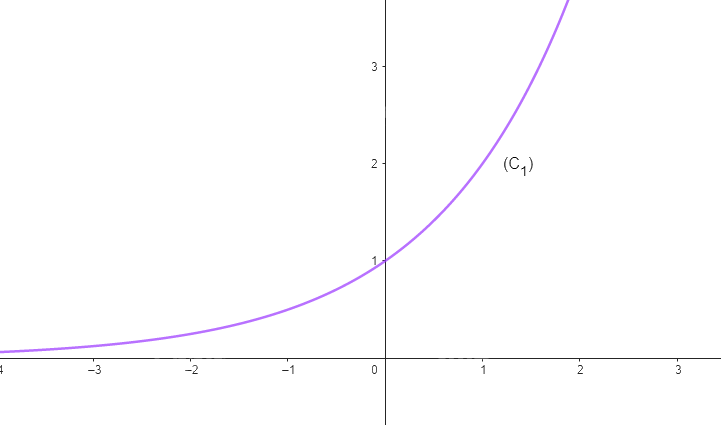
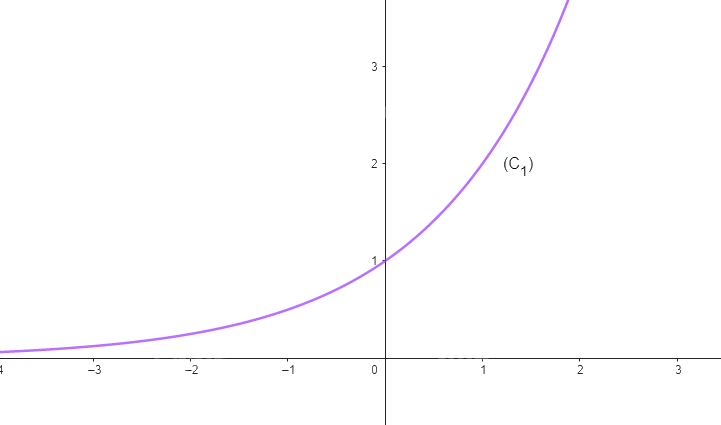
Cho hàm số \(y = {2^x}\) có đồ thị là (C1) và hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) có đồ thị (C2).
a) Hoàn thành bảng giá trị sau và biểu diễn trong mặt phẳng Oxy:

b) Vẽ đường cong nối các điểm thuộc (C1) (Theo thứ tự hoành độ tăng dần) và một đường cong khác nối các điểm thuộc (C2) (Theo thứ tự hoành độ tăng dần).
Phương pháp giải:
Thay x = -3, -2,… , 3 vào \(y = {2^x}\) và \(y = {\left( {\frac{1}{2}} \right)^x}\)
Lời giải chi tiết:
a,
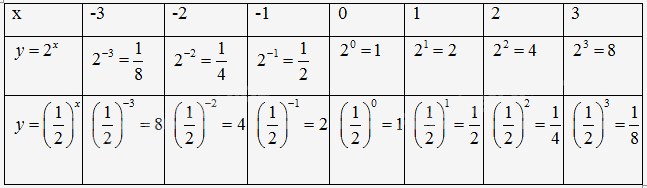
b)
Luyện tập 2
Đồ thị Hình 6.8 cho thấy số lượng hươu cao cổ trên thế giới suy giảm nghiêm trọng trong 30 năm qua (từ năm 1985 đến 2015) (nguồn: https://tuoitre.vn/huou-cao-co-sap-vao-danh-sach-loai-gap-nguy-hiem-20190428162017473.htm). Giả sử rằng số lượng hươu ở đây giảm theo hàm số \(n\left( t \right) = C.{a^t}\).
a) Tìm số lượng hươu vào năm 1985.
b) Tìm hàm số biểu diễn số lượng hươu sau t năm kể từ năm 1985.
c) Dự đoán số lượng hươu vào năm 2025.

Phương pháp giải:
a) Năm 1985 là t = 0, quan sát đồ thị khi t = 0 thì n bằng bao nhiêu.
b) Số lượng hươu mỗi năm là số lượng hươu năm 1985 trừ đi số lượng hươu giảm được tính theo hàm số \(n\left( t \right) = C.{a^t}\).
c) Kể từ năm 1985 đến 2025 là 40 năm nên t = 40. Thay t = 40 vào hàm số ở phần b.
Lời giải chi tiết:
a) Số lượng hươu năm 1985 là 152 nghìn con.
b) Ta có: \(C.{a^0} = n\left( 0 \right) \Leftrightarrow C = 152\)
\(\begin{array}{l}C.{a^{30}} = n\left( {30} \right)\\ \Leftrightarrow 152.{a^{30}} = 97,5\\ \Leftrightarrow {a^{30}} = \frac{{195}}{{304}}\\ \Leftrightarrow a = \sqrt[{30}]{{\frac{{195}}{{304}}}}\end{array}\)
\( \Rightarrow n\left( t \right) = 152.{\left( {\sqrt[{30}]{{\frac{{195}}{{304}}}}} \right)^t}\)
Hàm số biểu diễn lượng hươu sau t năm kể từ năm 1985 là: \(H\left( t \right) = 152 - 152.{\left( {\sqrt[{30}]{{\frac{{195}}{{304}}}}} \right)^t}\)
c) Kể từ năm 1985 đến 2025 là 40 năm nên t = 40
Số lượng hươu vào năm 2025 là: \(H\left( {40} \right) = 152 - 152.{\left( {\sqrt[{30}]{{\frac{{195}}{{304}}}}} \right)^{40}} \approx 67,914\) (nghìn con)
Giải mục 1 trang 14, 15 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải
Mục 1 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề quan trọng trong chương trình học. Trang 14 và 15 thường chứa các bài tập vận dụng kiến thức lý thuyết đã học để giải quyết các vấn đề cụ thể. Việc nắm vững phương pháp giải các bài tập này là vô cùng quan trọng để đạt kết quả tốt trong các bài kiểm tra và thi cử.
Nội dung chính của Mục 1 (trang 14, 15)
Để hiểu rõ hơn về nội dung của Mục 1, chúng ta cần xác định chủ đề chính mà nó đề cập đến. Thông thường, đây có thể là:
- Đạo hàm của hàm số: Tính đạo hàm, ứng dụng đạo hàm để xét tính đơn điệu, cực trị của hàm số.
- Giới hạn của hàm số: Tính giới hạn, ứng dụng giới hạn để xét tính liên tục của hàm số.
- Các phép biến hình: Phép tịnh tiến, phép quay, phép dời hình, phép vị tự.
- Vectơ trong không gian: Các phép toán vectơ, ứng dụng vectơ để giải quyết các bài toán hình học.
Phương pháp giải các bài tập trong Mục 1
Để giải quyết hiệu quả các bài tập trong Mục 1, các em cần nắm vững các bước sau:
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và các kết quả cần tìm.
- Xác định kiến thức cần sử dụng: Dựa vào yêu cầu của bài toán, xác định các kiến thức lý thuyết, công thức và định lý cần sử dụng.
- Lập kế hoạch giải: Xác định các bước giải cụ thể, các phép toán cần thực hiện và thứ tự thực hiện.
- Thực hiện giải: Thực hiện các phép toán theo kế hoạch đã lập, đảm bảo tính chính xác và logic.
- Kiểm tra lại kết quả: Kiểm tra lại kết quả đã tìm được, đảm bảo nó phù hợp với yêu cầu của bài toán và các dữ kiện đã cho.
Giải chi tiết các bài tập trang 14, 15 SGK Toán 11 tập 2
Dưới đây là giải chi tiết một số bài tập tiêu biểu trong Mục 1 trang 14, 15 SGK Toán 11 tập 2:
Bài 1: (Ví dụ minh họa)
Cho hàm số y = x2 - 2x + 3. Tính đạo hàm của hàm số.
Giải:
Áp dụng công thức đạo hàm của hàm số bậc hai, ta có:
y' = 2x - 2
Bài 2: (Ví dụ minh họa)
Tính giới hạn limx→2 (x2 - 4) / (x - 2)
Giải:
Ta có: limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 4
Lưu ý khi giải bài tập
Để đạt hiệu quả cao nhất khi giải bài tập, các em cần lưu ý:
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, định lý và công thức liên quan đến chủ đề đang học.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Sử dụng tài liệu tham khảo: Tham khảo các sách giáo khoa, sách bài tập, tài liệu trực tuyến để bổ sung kiến thức và tìm hiểu các phương pháp giải khác nhau.
- Hỏi thầy cô giáo: Nếu gặp khó khăn trong quá trình giải bài tập, hãy hỏi thầy cô giáo để được hướng dẫn và giải đáp.
Hy vọng với những hướng dẫn chi tiết trên, các em sẽ tự tin hơn khi giải các bài tập trong Mục 1 trang 14, 15 SGK Toán 11 tập 2. Chúc các em học tập tốt!