Bài 8.8 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Bài 8.8 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Bài 8.8 trang 63 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này giúp học sinh hiểu sâu hơn về các khái niệm và phương pháp đã học.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, cùng với các lưu ý quan trọng để bạn có thể tự tin giải quyết bài toán này và các bài tập tương tự.
Cho tứ diện ABCD biết ABC và BCD là hai tam giác cân có chung cạnh đáy BC . Gọi I là trung điểm cạnh BC. Chứng minh \(BC \bot (ADI)\).
Đề bài
Cho tứ diện ABCD biết ABC và BCD là hai tam giác cân có chung cạnh đáy BC . Gọi I là trung điểm cạnh BC. Chứng minh \(BC \bot (ADI)\).
Phương pháp giải - Xem chi tiết
Dựa vào tam giác cân để suy ra \(AI \bot BC\) và \(DI \bot BC\)
Lời giải chi tiết
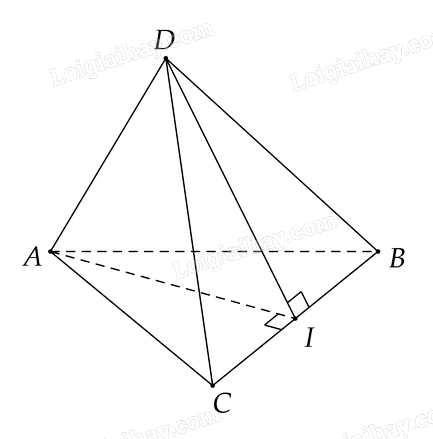
Vì \(\Delta ABC\) cân tại \(A\) và \(I\) là trung điểm của \(BC\) nên \(AI \bot BC\)
Vì \(\Delta DBC\) cân tại \(D\) và \(I\) là trung điểm của \(BC\) nên \(DI \bot BC\)
Ta có \(\left\{ \begin{array}{l}BC \bot AI\\BC \bot DI\end{array} \right. \Rightarrow BC \bot \left( {AID} \right)\)
Bài 8.8 trang 63 SGK Toán 11 tập 2 - Giải chi tiết và hướng dẫn
Bài 8.8 trang 63 SGK Toán 11 tập 2 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài toán này, chúng ta cần thực hiện các bước sau:
- Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
- Tính đạo hàm cấp nhất: Tính f'(x).
- Tìm các điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0 hoặc không xác định.
- Lập bảng biến thiên: Xác định dấu của f'(x) trên các khoảng xác định bởi các điểm tới hạn. Từ đó, xác định khoảng hàm số đồng biến, nghịch biến.
- Xác định cực trị: Dựa vào bảng biến thiên, xác định các điểm cực đại, cực tiểu của hàm số.
Ví dụ minh họa (giả sử hàm số là f(x) = x^3 - 3x^2 + 2):
Bước 1: Tập xác định: Hàm số f(x) = x^3 - 3x^2 + 2 xác định trên R.
Bước 2: Đạo hàm cấp nhất: f'(x) = 3x^2 - 6x
Bước 3: Điểm tới hạn: Giải phương trình 3x^2 - 6x = 0, ta được x = 0 hoặc x = 2.
Bước 4: Bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Bước 5: Cực trị:
- Tại x = 0, f'(x) đổi dấu từ dương sang âm, nên x = 0 là điểm cực đại. Giá trị cực đại là f(0) = 2.
- Tại x = 2, f'(x) đổi dấu từ âm sang dương, nên x = 2 là điểm cực tiểu. Giá trị cực tiểu là f(2) = -2.
Lưu ý quan trọng khi giải Bài 8.8
- Luôn kiểm tra tập xác định của hàm số trước khi tính đạo hàm.
- Chú ý đến các điểm mà đạo hàm không xác định, vì chúng cũng có thể là điểm tới hạn.
- Sử dụng bảng biến thiên để xác định khoảng đồng biến, nghịch biến và cực trị một cách chính xác.
- Thực hành nhiều bài tập tương tự để nắm vững phương pháp giải.
Tại sao nên chọn tusach.vn để học Toán 11?
- Lời giải chi tiết, dễ hiểu: Chúng tôi cung cấp lời giải bài tập Toán 11 một cách rõ ràng, dễ theo dõi, giúp bạn hiểu bản chất của vấn đề.
- Đội ngũ giáo viên giàu kinh nghiệm: Các lời giải được biên soạn bởi các giáo viên Toán 11 có nhiều năm kinh nghiệm giảng dạy.
- Cập nhật liên tục: Chúng tôi luôn cập nhật lời giải mới nhất cho các bài tập trong SGK Toán 11.
- Giao diện thân thiện, dễ sử dụng: Bạn có thể dễ dàng tìm kiếm và xem lời giải bài tập trên mọi thiết bị.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập Toán 11 hữu ích và đạt kết quả cao trong học tập!