Giải mục 1 trang 73, 74 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 73, 74 SGK Toán 11 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 73, 74 sách giáo khoa Toán 11 tập 2. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những bài giải chính xác, dễ hiểu, giúp các em tự tin hơn trong quá trình học tập.
Mục 1 này tập trung vào việc... (nội dung cụ thể của mục 1). Hãy cùng nhau khám phá và chinh phục những bài toán thú vị này nhé!
Cho đường thẳng a và một điểm O không thuộc a. H là hình chiếu của O trên đường thẳng a và M là một điểm bất kì thuộc a (Hình 8.49).
Hoạt động 1
Cho đường thẳng a và một điểm O không thuộc a. H là hình chiếu của O trên đường thẳng a và M là một điểm bất kì thuộc a (Hình 8.49). Trong hai điểm H và M điểm nào có khoảng cách đến O ngắn hơn? Vì sao?
Phương pháp giải:
Quan hệ giữa đường xiên và hình chiếu.
Lời giải chi tiết:
Trong điểm H và M thì điểm H gần O hơn.
Vì tam giác OHM vuông tại H nên ta có OH < OM (quan hệ giữa đường xiên và hình chiếu)
Luyện tập 1
Cho hình lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC. Tính khoảng cách từ G đến đường thẳng A’C’.
Phương pháp giải:
Cho O không thuộc a. H là hình chiếu của O trên a. Độ dài OH là khoảng cách từ O đến a.
Lời giải chi tiết:

Gọi G’ là trọng tâm tam giác A’B’C’, M là trung điểm AC, M’ là trung điểm của A’C’
Ta có: GG’ vuông góc với (A’B’C’) nên GG’ vuông góc với A’C’
G’M’ là trung tuyến của A’B’C’ nên G’M’ vuông góc với A’C’ (Vì tam giác A’B’C’ đều)
Suy ra (GG’M’) vuông góc với A’C’
\( \Rightarrow \)GM’ vuông góc với A’C’
Vậy GM’ là khoảng cách từ G đến A’C’
Tam giác A’B’C’ đều cạnh a nên B’M’ = \(B'M' = \frac{{\sqrt 3 }}{2}a\)
Suy ra G’M’ = \(G'M' = \frac{{\sqrt 3 }}{6}a\)
Xét tam giác vuông GM’G’ tại M’ có:
\(GM' = \sqrt {GG{'^2} + G'M{'^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\frac{{\sqrt 3 }}{6}a} \right)}^2}} = \frac{{7\sqrt 3 }}{6}a\)
Hoạt động 2
Cho mặt phẳng \(\left( \alpha \right)\) và O là một điểm không thuộc \(\left( \alpha \right)\). H là hình chiếu của O trên \(\left( \alpha \right)\). Lấy tuy ý điểm M thuộc \(\left( \alpha \right)\). Trong các diểm H và M, điểm nào có khoảng cách đến O ngắn hơn? Vì sao?

Phương pháp giải:
Quan hệ đường xiên và hình chiếu.
Lời giải chi tiết:
Tam giác OHM vuông tại H nên OH < OM (Quan hệ đường xiên và hình chiếu).
Luyện tập 2
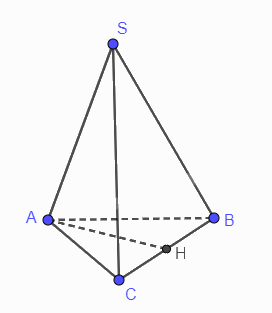
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = 2a; tam giác ABC đều bằng a. Tính khoảng cách từ A đến mặt phẳng (SBC).
Phương pháp giải:
Tìm khoảng cách từ M đến (P):
+ Tìm (Q) chứa M và vuông góc với (P) theo giao tuyến d.
+ Từ M hạ MH vuông góc với d (H thuộc d).
+ Khi đó MH chính là khoảng cách cần tìm.
Lời giải chi tiết:

Gọi H là trung điểm của BC
Tam giác ABC đều nên AH vuông góc với BC
Suy ra \(d\left( {A,\left( {SBC} \right)} \right) = AH\)
\(AH = \sqrt {A{C^2} - C{H^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = \sqrt 3 a\)
Giải mục 1 trang 73, 74 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải
Mục 1 trang 73, 74 SGK Toán 11 tập 2 thuộc chương trình học về đạo hàm, một trong những khái niệm quan trọng nhất của Toán học. Nắm vững kiến thức về đạo hàm là nền tảng để giải quyết nhiều bài toán phức tạp hơn trong các chương trình học tiếp theo.
Nội dung chính của Mục 1
Mục 1 tập trung vào việc:
- Ôn tập lại khái niệm đạo hàm của hàm số tại một điểm.
- Tìm hiểu về đạo hàm của các hàm số đơn giản như hàm số bậc hai, hàm số mũ, hàm số logarit.
- Luyện tập các bài toán tính đạo hàm bằng định nghĩa và các quy tắc đạo hàm cơ bản.
Các bài tập trong Mục 1
Các bài tập trong mục 1 được thiết kế để giúp học sinh:
- Củng cố kiến thức về đạo hàm.
- Rèn luyện kỹ năng tính đạo hàm.
- Áp dụng đạo hàm vào việc giải quyết các bài toán thực tế.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 1 trang 73, 74 SGK Toán 11 tập 2:
Bài 1: Tính đạo hàm của hàm số f(x) = x2 + 2x + 1
Lời giải:
Áp dụng quy tắc đạo hàm của tổng và đạo hàm của hàm số lũy thừa, ta có:
f'(x) = 2x + 2
Bài 2: Tính đạo hàm của hàm số g(x) = ex
Lời giải:
Đạo hàm của hàm số mũ ex là chính nó:
g'(x) = ex
Bài 3: Tính đạo hàm của hàm số h(x) = ln(x)
Lời giải:
Đạo hàm của hàm số logarit ln(x) là:
h'(x) = 1/x
Mẹo giải nhanh các bài tập về đạo hàm
Để giải nhanh các bài tập về đạo hàm, bạn có thể áp dụng các mẹo sau:
- Nắm vững các quy tắc đạo hàm cơ bản.
- Sử dụng bảng đạo hàm để tra cứu nhanh các đạo hàm của các hàm số thường gặp.
- Phân tích bài toán để xác định phương pháp giải phù hợp.
Tài liệu tham khảo hữu ích
Để học tốt môn Toán 11, bạn có thể tham khảo các tài liệu sau:
- Sách giáo khoa Toán 11 tập 2.
- Sách bài tập Toán 11 tập 2.
- Các trang web học Toán trực tuyến uy tín như tusach.vn.
Hy vọng với những hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải các bài tập về đạo hàm. Chúc các em học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = ex | f'(x) = ex |
| f(x) = ln(x) | f'(x) = 1/x |
| Bảng đạo hàm cơ bản | |