Giải mục 3 trang 69, 70, 71, 72, 73 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 69, 70, 71, 72, 73 SGK Toán 11 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 69, 70, 71, 72, 73 sách giáo khoa Toán 11 tập 1. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em hiểu rõ kiến thức và tự tin giải quyết các bài tập.
Mục 3 này tập trung vào các kiến thức quan trọng về... (điền kiến thức chính của mục 3 vào đây). Chúng tôi sẽ cung cấp lời giải từng bước, dễ hiểu, kèm theo các lưu ý quan trọng để các em có thể nắm vững kiến thức.
Cho hàm số \(y = f(x) = \frac{1}{x}\)
Hoạt động 6
Cho hàm số \(y = f(x) = \frac{1}{x}\)
a, Tìm tập xác định của hàm số.
b, Tính giá trị của hàm số tại các điểm trong bảng giá trị sau:
c, Nhận xét gì về giá trị của f(x) khi x dần đến \( + \infty \)? Khi x dần đến \( - \infty \)?
Phương pháp giải:
Tập xác định là các giá trị của x để hàm số có nghĩa.
Thay giá trị của x vào hàm số để được các giá trị của f(x) tương ứng.
Lời giải chi tiết:
a, Tập xác định: R\{0}.
b, Thay lần lượt các giá trị của x vào f(x) ta được:
\(\)x dần đến \( - \infty \) thì f(x)=0
\(f( - {10^8}) = \frac{1}{{ - {{10}^8}}} = - {10^{ - 8}}\)
\(f(10) = \frac{1}{{10}}\)
\(f( - {10^3}) = \frac{1}{{ - {{10}^3}}} = - {10^{ - 3}}\)
\(f(1000) = \frac{1}{{1000}} = {10^{ - 3}}\)
\(f( - {10^2}) = \frac{1}{{ - {{10}^2}}} = - {10^{ - 2}}\)
\(f(100000) = \frac{1}{{100000}} = {10^{ - 5}}\)
\(f( - 10) = \frac{1}{{ - 10}} = \frac{{ - 1}}{{10}}\)
\(f({10^9}) = \frac{1}{{{{10}^9}}} = {10^{ - 9}}\)
x dần đến \( + \infty \) thì f(x)=0.

c, Khi x dần đến và x dần đến thì f(x)=0.
Luyện tập 7
Cho hàm số \(f(x) = \frac{{\sqrt {{x^2} + 1} }}{x}\). Tìm \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to + \infty } f(x)\).
Phương pháp giải:
Đưa x ra khỏi dấu căn để chia cả tử và mẫu cho x.
Với x dần đến \( - \infty \) thì |x| = -x
Với x dần đến \( + \infty \) thì |x| = x.
Lời giải chi tiết:
Hàm số có tập xác định là \(( - \infty ;0) \cup (0; + \infty )\)
Giả sử \(({x_n})\) là một dãy số bất kì thỏa mãn \({x_n} < 0\) và \(\lim {x_n} = - \infty \)
Ta có \(\lim f({x_n}) = \frac{{\sqrt {x_n^2 + 1} }}{{{x_n}}} = \lim \frac{{\left| {{x_n}} \right|.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim \frac{{ - {x_n}.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim ( - \sqrt {1 + \frac{1}{{x_n^2}}} ) = - 1\)
Giả sử \(({x_n})\) là một dãy số bất kì thỏa mãn \({x_n} > 0\) và \(\lim {x_n} = + \infty \)
Ta có \(\lim f({x_n}) = \frac{{\sqrt {x_n^2 + 1} }}{{{x_n}}} = \lim \frac{{\left| {{x_n}} \right|.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim \frac{{{x_n}.\sqrt {1 + \frac{1}{{x_n^2}}} }}{{{x_n}}} = \lim \sqrt {1 + \frac{1}{{x_n^2}}} = 1\)
Vậy \(\mathop {\lim }\limits_{x \to - \infty } f(x) = - 1\) và \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 1\).
Luyện tập 8
Tìm \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} - 4} }}{{x + 5}}\).
Phương pháp giải:
Đưa x ra khỏi dấu căn để chia cả tử và mẫu cho x.
Với x dần đến \( - \infty \) thì |x| = -x
Lời giải chi tiết:
Hàm số có tập xác định là \(( - \infty ; - 5) \cup ( - 5; + \infty )\)
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} - 4} }}{{x + 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\left| x \right|.\sqrt {1 - \frac{4}{{{x^2}}}} }}{{x + 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {1 - \frac{4}{{{x^2}}}} }}{{x + 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - \sqrt {1 - \frac{4}{{{x^2}}}} }}{{1 + \frac{5}{x}}}\)
Vì \(\mathop {\lim }\limits_{x \to - \infty } - \sqrt {1 - \frac{4}{{{x^2}}}} = - 1\) , lim 1=1 và \(\mathop {\lim }\limits_{x \to - \infty } \frac{5}{x} = 0\) ta có:
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - \sqrt {1 - \frac{4}{{{x^2}}}} }}{{1 + \frac{5}{x}}} = - 1\).
Hoạt động 7
Cho hàm số \(f(x) = {x^2}\) và dãy số \(({x_n})\) với \({x_n} = n + 1\)
a, Tìm \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}\)
b, Tính \(f({x_n})\) theo n và tìm \({\mathop{\rm l}\nolimits} {\rm{im f(}}{{\rm{x}}_n})\).
Phương pháp giải:
a, Thay \({x_n} = n + 1\) để tìm \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}\)
b, Thay \({x_n} = n + 1\) vào hàm số \(f(x) = {x^2}\) để tìm \(f({x_n})\)
Dựa vào câu a để xác định \({\mathop{\rm l}\nolimits} {\rm{im f(}}{{\rm{x}}_n})\).
Lời giải chi tiết:
a, Ta có: \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = \lim (n + 1)\)
\(\mathop {\lim }\limits_{n \to - \infty } (n + 1) = - \infty \) và \(\mathop {\lim }\limits_{n \to + \infty } (n + 1) = + \infty \).
b, Thay \({x_n} = n + 1\) vào hàm số \(f(x) = {x^2}\) ta được:
\(f({x_n}) = {(n + 1)^2}\)
\(\mathop {\lim }\limits_{n \to - \infty } {\rm{f(}}{{\rm{x}}_n}) = \mathop {\lim }\limits_{n \to - \infty } {(n + 1)^2} = + \infty \) và \(\mathop {\lim }\limits_{n \to + \infty } {\rm{f(}}{{\rm{x}}_n}) = \mathop {\lim }\limits_{n \to + \infty } {(n + 1)^2} = + \infty \).
Luyện tập 9
Tìm \(\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1}}{x}\)
Phương pháp giải:
Chia tử cho mẫu để tính giới hạn
Lời giải chi tiết:
Hàm số \(f(x) = \frac{{{x^2} + 1}}{x} = x + \frac{1}{x}\) có tập xác định là \(( - \infty ;0) \cup (0; + \infty )\)
\(\forall ({x_n}),{x_n} < 0\)và \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = - \infty \), ta có \(\lim f({x_n}) = \lim ({x_n} + \frac{1}{{{x_n}}}) = {\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}(1 + \frac{1}{{x_n^2}})\)
Vì \({\mathop{\rm l}\nolimits} {\rm{im x}}_n^2 = + \infty \) nên \(\lim \frac{1}{{x_n^2}} = 0\). Suy ra \(\lim (1 + \frac{1}{{x_n^2}}) = 1\)
Vì \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = - \infty \) và \(\lim (1 + \frac{1}{{x_n^2}}) = 1\) nên \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n}(1 + \frac{1}{{x_n^2}}) = - \infty \)
Vậy \(\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1}}{x} = - \infty \).
Hoạt động 8
Cho hàm số \(f(x) = \frac{{x - 1}}{{x + 1}}\) và g(x)=x+1
a, Tìm \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to + \infty } g(x)\)
b, Tìm \(\mathop {\lim }\limits_{x \to + \infty } {\rm{[}}f(x).g(x){\rm{]}}\).
Phương pháp giải:
a, Với f(x) chia tử cho mẫu để tìm giới hạn
Với g(x) thì \(\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } (x + 1) = + \infty \)
b, Tính f(x). g(x) và dựa vào câu a xác định \(\mathop {\lim }\limits_{x \to + \infty } {\rm{[}}f(x).g(x){\rm{]}}\)
Lời giải chi tiết:
a, Hàm số \(f(x) = \frac{{x - 1}}{{x + 1}} = 1 - \frac{2}{{x + 1}}\) có tập xác định \(( - \infty , - 1) \cup ( - 1; + \infty )\)
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } (1 - \frac{2}{{x + 1}}) = 1\)
\(\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } (x + 1) = + \infty \)
b, Ta có: \(f(x).g(x) = \frac{{x - 1}}{{x + 1}}.(x + 1) = x - 1\)
\(\mathop {\lim }\limits_{x \to + \infty } f(x).g(x) = \mathop {\lim }\limits_{x \to + \infty } (x - 1) = + \infty \).
Luyện tập 10
Tìm \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt {{x^2} + 2x} }}\).
Phương pháp giải:
Xác định \(\mathop {\lim }\limits_{x \to {0^ + }} \sqrt {{x^2} + 2x} \) để tìm \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt {{x^2} + 2x} }}\)
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to {0^ + }} \sqrt {{x^2} + 2x} \)=0 và \(\sqrt {{x^2} + 2x} > 0,\forall x > 0\) nên \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt {{x^2} + 2x} }} = + \infty \).
Vận dụng
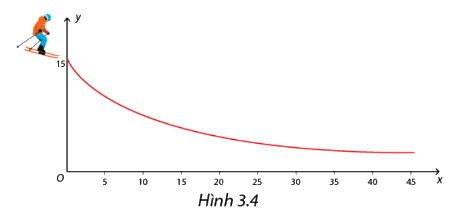
Trong một cuộc thi các môn thể thao trên tuyết, người ta muốn thiết kế một đường trượt bằng bang cho nội dung đổ dốc tốc độ đường dài

Vận động viên sẽ xuất phát từ vị trí (0; 15) cao 15 m so với mặt đất (trục 0x) . Đường trượt phải thỏa mãn yêu cầu là càng ra xa thì càng gần mặt đất để tiết kiệm lượng tuyết nhân tạo. Một nhà thiết kế đề nghị sử dụng đường cong là đồ thị \(y = f(x) = \frac{{150}}{{x + 10}}\) với \(x \ge 0\). Hãy kiểm tra xem hàm số y=f(x) có thỏa mãn các điều kiện dưới đây hay không:
a, Có đồ thị đi qua điểm (0,15)
b, Giảm trên \(\left[ {0, + \infty } \right]\)
c, Càng ra xa ( x càng lớn), đồ thị càng gần trục Ox với khoảng cách nhỏ tùy ý.
Phương pháp giải:
a, Thay tọa độ (0,15) vào hàm số để kiểm tra điểm có thuộc hàm số hay không?
b, Nhận xét với x càng tăng thì giá trị f(x) càng giảm
c, Tính lim f(x) khi x dần đến \( + \infty \)
Lời giải chi tiết:
a, Thay x=0 vào hàm số \(y = f(x) = \frac{{150}}{{x + 10}}\) ta được:
\(y = \frac{{150}}{{0 + 10}} = \frac{{150}}{{10}} = 15\)
Vậy điểm (0,15) thuộc đồ thị hàm số.
b, Nhận thấy khi x càng tăng thì giá trị hàm số càng giảm. Vậy hàm số \(y = f(x) = \frac{{150}}{{x + 10}}\) giảm trên \(\left[ {0, + \infty } \right]\)
c, Ta có : \(\mathop {\lim }\limits_{x \to + \infty } \frac{{150}}{{x + 10}} = 0\)
Vậy càng ra xa ( x càng lớn), đồ thị càng gần trục Ox với khoảng cách nhỏ tùy ý.
Giải mục 3 trang 69, 70, 71, 72, 73 SGK Toán 11 tập 1 - Cùng khám phá
Mục 3 trong SGK Toán 11 tập 1 là một phần quan trọng, đặt nền móng cho các kiến thức nâng cao hơn trong chương trình học. Nhiều học sinh gặp khó khăn khi giải các bài tập trong mục này, đặc biệt là các bài tập đòi hỏi sự vận dụng linh hoạt của các công thức và định lý đã học. Tusach.vn ra đời với mục tiêu hỗ trợ các em học sinh giải quyết những khó khăn này.
Nội dung chính của Mục 3 SGK Toán 11 tập 1
Mục 3 thường bao gồm các nội dung sau (điền nội dung cụ thể của mục 3 vào đây, ví dụ):
- Định nghĩa về...
- Các tính chất của...
- Ứng dụng của... trong giải toán
- Các dạng bài tập thường gặp
Giải chi tiết các bài tập trang 69, 70, 71, 72, 73
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 3, trang 69, 70, 71, 72, 73 SGK Toán 11 tập 1:
Bài 1 (Trang 69)
Đề bài: (Viết đề bài vào đây)
Lời giải: (Viết lời giải chi tiết vào đây, kèm theo các bước giải thích rõ ràng)
Bài 2 (Trang 70)
Đề bài: (Viết đề bài vào đây)
Lời giải: (Viết lời giải chi tiết vào đây, kèm theo các bước giải thích rõ ràng)
Bài 3 (Trang 71)
Đề bài: (Viết đề bài vào đây)
Lời giải: (Viết lời giải chi tiết vào đây, kèm theo các bước giải thích rõ ràng)
Bài 4 (Trang 72)
Đề bài: (Viết đề bài vào đây)
Lời giải: (Viết lời giải chi tiết vào đây, kèm theo các bước giải thích rõ ràng)
Bài 5 (Trang 73)
Đề bài: (Viết đề bài vào đây)
Lời giải: (Viết lời giải chi tiết vào đây, kèm theo các bước giải thích rõ ràng)
Lưu ý quan trọng khi giải bài tập Mục 3
Để giải tốt các bài tập trong Mục 3, các em cần:
- Nắm vững các định nghĩa, tính chất và công thức liên quan.
- Đọc kỹ đề bài, xác định đúng yêu cầu của bài toán.
- Vận dụng linh hoạt các kiến thức đã học để giải quyết bài toán.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Đồng hành cùng học sinh trên mọi hành trình
Tusach.vn không chỉ cung cấp lời giải chi tiết mà còn cung cấp nhiều tài liệu học tập hữu ích khác, giúp các em học sinh học tập hiệu quả hơn. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu và hỗ trợ học tập nhé!
Chúc các em học tập tốt!