Giải mục 1 trang 80 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 80 SGK Toán 11 tập 2 - Cùng khám phá
Chào mừng bạn đến với lời giải chi tiết mục 1 trang 80 SGK Toán 11 tập 2 trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ bạn trong quá trình học tập môn Toán 11.
Viết công thức tính thể tích khối lăng trụ đứng tam giác (Hình 8.68)
Hoạt động 1
Viết công thức tính thể tích khối lăng trụ đứng tam giác (Hình 8.68) và khối lăng trụ đứng tứ giác (Hình 8.69) theo diện tích đáy S và đường cao h của nó.
Phương pháp giải:
V = S.h
Lời giải chi tiết:
Công thức tính thể tích khối lăng trụ đứng: V = S.h
Luyện tập 1
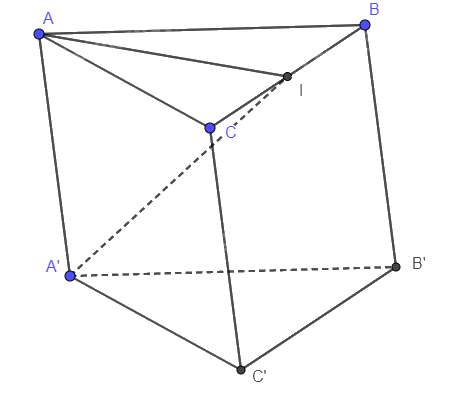
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a , góc giữa cạnh bên và mặt đáy bằng 300. Hình chiếu của A’ trên (ABC) là trung điểm I của cạnh BC. Tính thể tích khối lăng trụ này.
Phương pháp giải:
Công thức tính thể tích khối lăng trụ: V = S.h
S: diện tích đáy, h: chiều cao
Lời giải chi tiết:

Gọi I là trung điểm BC
\(AI = \sqrt {A{C^2} - I{C^2}} = \sqrt {{a^2} - {{\left( {\frac{1}{2}a} \right)}^2}} = \frac{{\sqrt 3 }}{2}a\)
Tam giác AB đều nên AI vuông góc với BC hay AI vuông góc với (ABC)
Suy ra \(\widehat {\left( {AA',\left( {ABC} \right)} \right)} = \widehat {A'AI} = {30^0}\)
I là hình chiếu của A’ trên (ABC) nên A’I vuông góc với BC
Suy ra tam giác A’AI vuông tại I có:
\(\tan {30^0} = \frac{{A'I}}{{AI}} = \frac{{A'I}}{{\frac{{\sqrt 3 }}{2}a}} \Rightarrow A'I = \frac{1}{2}a\)
\(V = {S_{\Delta ABC}}.A'I = \frac{1}{2}AI.BC.A'I = \frac{1}{2}.\frac{{\sqrt 3 }}{2}a.a.\frac{1}{2}a = \frac{{\sqrt 3 }}{8}{a^3}\)
Giải mục 1 trang 80 SGK Toán 11 tập 2 - Cùng khám phá: Hướng dẫn chi tiết và dễ hiểu
Mục 1 trang 80 SGK Toán 11 tập 2 thường xoay quanh các bài toán về đạo hàm của hàm số. Đây là một phần kiến thức quan trọng, nền tảng cho việc học tập các chương trình Toán học nâng cao hơn. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết, kèm theo các lưu ý quan trọng để bạn có thể nắm vững kiến thức.
Nội dung chính của Mục 1 trang 80 SGK Toán 11 tập 2
- Bài 1: Tính đạo hàm của các hàm số sau: ... (Liệt kê các hàm số cụ thể)
- Bài 2: Tìm đạo hàm của hàm số y = ... (Ví dụ hàm số)
- Bài 3: Áp dụng quy tắc đạo hàm để giải các bài toán thực tế.
Phương pháp giải các bài tập về đạo hàm
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn cần nắm vững các quy tắc đạo hàm cơ bản, bao gồm:
- Quy tắc đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Quy tắc đạo hàm của hàm hợp.
- Đạo hàm của các hàm số lượng giác, mũ, logarit.
Ví dụ minh họa: Giải Bài 1 trang 80 SGK Toán 11 tập 2
Đề bài: Tính đạo hàm của hàm số y = x3 + 2x2 - 5x + 1.
Lời giải:
Áp dụng quy tắc đạo hàm của tổng, ta có:
y' = (x3)' + (2x2)' - (5x)' + (1)'
y' = 3x2 + 4x - 5 + 0
y' = 3x2 + 4x - 5
Lưu ý quan trọng khi giải bài tập về đạo hàm
- Luôn kiểm tra lại kết quả sau khi tính đạo hàm.
- Sử dụng các quy tắc đạo hàm một cách chính xác.
- Chú ý đến các trường hợp đặc biệt, ví dụ như đạo hàm của hàm hợp.
Bảng tổng hợp các công thức đạo hàm thường dùng
| Hàm số y | Đạo hàm y' |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |
Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải các bài tập về đạo hàm trong Mục 1 trang 80 SGK Toán 11 tập 2. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi trong phần bình luận bên dưới. Chúc bạn học tập tốt!
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục kiến thức Toán học.