Giải mục 2 trang 67, 68, 69 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 67, 68, 69 SGK Toán 11 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 67, 68, 69 SGK Toán 11 tập 1. Bài viết này được tusach.vn biên soạn nhằm hỗ trợ các em trong quá trình học tập và ôn luyện môn Toán.
Chúng tôi sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin giải quyết các bài tập tương tự.
Cho hàm số (f(x) = left{ begin{array}{l}x + 2,x ge 1\x - 4,x < 1end{array} right.) và hai dãy số (({u_n})) và (({v_n})) với ({u_n} = 1 + frac{1}{n}), ({v_n} = 1 - frac{1}{n})
Hoạt động 4
Cho hàm số \(f(x) = \left\{ \begin{array}{l}x + 2,x \ge 1\\x - 4,x < 1\end{array} \right.\) và hai dãy số (\({u_n}\)) và (\({v_n}\)) với \({u_n} = 1 + \frac{1}{n}\), \({v_n} = 1 - \frac{1}{n}\)
a, So sánh \({u_n},{v_n}\) với 1 và tìm \(\lim {u_n}\), \(\lim {v_n}\).
b, Tính \(f({u_n})\) và \(f({v_n})\) theo n.
c, Tìm lim\(f({u_n})\) và lim\(f({v_n})\).
Phương pháp giải:
a, Xác định \(\lim \frac{1}{n}\) để so sánh \({u_n},{v_n}\) với 1 và tìm \(\lim {u_n}\), \(\lim {v_n}\).
b, Thay \({u_n} = 1 + \frac{1}{n}\), \({v_n} = 1 - \frac{1}{n}\) để tính \(f({u_n})\) và \(f({v_n})\).
c, Sử dụng câu a,b để tìm lim\(f({u_n})\) và lim\(f({v_n})\).
Lời giải chi tiết:
a, Ta có \(\lim \frac{1}{n} = 0\) và \(\frac{1}{n} > 0\) nên:
\({u_n} = 1 + \frac{1}{n} > 1\) và \({v_n} = 1 - \frac{1}{n} < 1\)
\(\lim {u_n} = \lim (1 + \frac{1}{n}) = 1\) và \(\lim {v_n} = \lim (1 - \frac{1}{n}) = 1\).
b, Với \({u_n} > 1\) thay x=\({u_n}\) vào f(x)=x+2 ta được:
\(f({u_n}) = {u_n} + 2 = 1 + \frac{1}{n} + 2 = 3 + \frac{1}{n}\).
Với \({v_n} < 1\) thay x=\({v_n}\) vào f(x) = x-4 ta được:
\(f({v_n}) = {v_n} - 4 = 1 - \frac{1}{n} - 4 = - 3 - \frac{1}{n}\).
c, Ta có: \(\lim f({u_n}) = \lim (3 + \frac{1}{n}) = 3\).
\(\lim f({v_n}) = \lim ( - 3 - \frac{1}{n}) = - 3\).
Luyện tập 4
Cho hàm số \(f(x) = \left\{ \begin{array}{l}{x^2} + 1,x \ge 1\\\frac{{{x^2} - 1}}{{x + 1}},x < 1\end{array} \right.\). Tính \(\mathop {\lim }\limits_{x \to {1^ + }} f(x)\)và \(\mathop {\lim }\limits_{x \to {1^ - }} f(x)\)
Phương pháp giải:
\(\mathop {\lim }\limits_{x \to - {1^ + }} f(x) = \lim ({x_n}^2 + 1)\)
\(\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \lim \frac{{{x_n}^2 - 1}}{{{x_n} + 1}}\)
Lời giải chi tiết:
Giả sử \(({x_n})\) là một dãy số bất kì mà \({x_n} > - 1\) và \(\lim {x_n} = - 1\), ta có \(f\left( {{x_n}} \right) = x_n^2 + 1\).
Vậy\(\mathop {\lim }\limits_{x \to - {1^ + }} f(x)\) =\(\lim f({x_n}) = {( - 1)^2} + 1 = 2\).
Giả sử \(({x_n})\) là một dãy số bất kì mà \({x_n} < - 1\) và \(\lim {x_n} = - 1\), ta có \(f({x_n}) = \frac{{x_n^2 - 1}}{{{x_n} + 1}} = \frac{{({x_n} - 1)({x_n} + 1)}}{{{x_n} + 1}} = {x_n} - 1\)
Vậy \(\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \)\(\lim f({x_n}) = - 1 - 1 = - 2\).
Luyện tập 5
Cho hàm số \(f(x) = \left\{ \begin{array}{l}2ax + 6,x \ge - 2\\\frac{{{x^2} - 4}}{{x + 2}},x < - 2\end{array} \right.\). Tìm a, biết rằng tồn tại \(\mathop {\lim }\limits_{x \to - 2} f(x)\)
Phương pháp giải:
\(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ + }} (2ax + 6) = - 4a + 6\)
\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{{x^2} - 4}}{{x + 2}}\mathop { = \lim }\limits_{x \to - {2^ - }} (x - 2) = - 4\)
Cho \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} f(x)\) để tìm giá trị của a.
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ + }} (2ax + 6) = - 4a + 6\)
\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{{x^2} - 4}}{{x + 2}}\mathop { = \lim }\limits_{x \to - {2^ - }} (x - 2) = - 4\)
Để tồn tại \(\mathop {\lim }\limits_{x \to - 2} f(x)\) thì \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} f(x) \Leftrightarrow - 4a + 6 = - 4 \Leftrightarrow - 4a = - 10 \Leftrightarrow a = \frac{5}{2}\)
Vậy \(a = \frac{5}{2}\).
Hoạt động 5
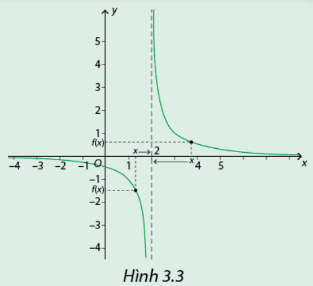
Đồ thị hàm số \(y = f(x) = \frac{1}{{x - 2}}\) được cho trong hình 3.3
a, Nếu M(x;f(x)) là một điểm trên đồ thị, hãy dự đoán giá trị của f(x) khi x dần đến 2 theo phía phải, theo phía trái.
b, \(({x_n})\)là một dãy số bất kì mà \({x_n} < 2\) và \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = 2\).Tính \(f({x_n})\) và \(\lim f({x_n})\).
Phương pháp giải:
a, Dựa vào phần đồ thị bên phải để xác định giá trị của f(x) khi x gần đến 2 theo phía phải và phần đồ thị bên trái để xác định giá trị của f(x) khi x gần đến 2 theo phía trái.
b, Thay \(x = {x_n}\) để tính \(f({x_n})\).
Tìm \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\).
Lời giải chi tiết:
a, Dự đoán: Khi x gần đến 2 theo phía phải thì f(x) gần đến \( + \infty \)
Khi x gần đến 2 theo phía trái thì f(x) gần đến \( - \infty \).
b, Thay \(x = {x_n}\) vào f(x) ta được : \(f({x_n}) = \frac{1}{{{x_n} - 2}}\)
Cho dãy số \(({x_n})\) với \({x_n} > 2\) và \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = 2\), lim1=1 ta có:
\(\lim f({x_n}) = + \infty \)
Cho dãy số \(({x_n})\) với \({x_n} < 2\) và \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = 2\), lim 1=1 ta có:
\(\lim f({x_n}) = - \infty \).
Luyện tập 6
Tìm \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{1}{{2 - x}}\) và \(\mathop {\lim }\limits_{x \to {4^ + }} \frac{1}{{x - 4}}\).
Phương pháp giải:
Áp dụng định lí \(\mathop {\lim }\limits_{x \to {a^ + }} \frac{1}{{x - a}} = + \infty \) và \(\mathop {\lim }\limits_{x \to {a^ - }} \frac{1}{{x - a}} = - \infty \) với mọi số thực a.
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{1}{{2 - x}} = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - 1}}{{x - 2}} = + \infty \)
\(\mathop {\lim }\limits_{x \to {4^ + }} \frac{1}{{x - 4}} = + \infty \)
Giải mục 2 trang 67, 68, 69 SGK Toán 11 tập 1: Tổng quan và Phương pháp giải
Mục 2 của SGK Toán 11 tập 1 thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 11.
Nội dung chính của Mục 2:
- Phép tịnh tiến: Định nghĩa, tính chất, và ứng dụng trong việc giải các bài toán hình học.
- Phép quay: Định nghĩa, tính chất, và cách xác định tâm quay, góc quay.
- Phép đối xứng trục: Định nghĩa, tính chất, và cách xác định trục đối xứng.
- Phép đối xứng tâm: Định nghĩa, tính chất, và cách xác định tâm đối xứng.
- Biến hình: Khái niệm biến hình, các loại biến hình, và mối liên hệ giữa chúng.
Hướng dẫn giải bài tập trang 67, 68, 69 SGK Toán 11 tập 1:
Để giải các bài tập trong mục này, các em cần:
- Nắm vững định nghĩa và tính chất của từng phép biến hình.
- Xác định đúng các yếu tố quan trọng của phép biến hình (ví dụ: tâm quay, góc quay, trục đối xứng, tâm đối xứng).
- Sử dụng các công thức và định lý liên quan để tính toán và chứng minh.
- Vẽ hình minh họa để dễ dàng hình dung và giải quyết bài toán.
Giải chi tiết các bài tập cụ thể:
Dưới đây là giải chi tiết một số bài tập tiêu biểu trong mục 2 trang 67, 68, 69 SGK Toán 11 tập 1:
Bài 1: (Trang 67)
Cho điểm A(1; 2). Tìm ảnh của điểm A qua phép tịnh tiến theo vectơ v = (3; -1).
Giải: Gọi A'(x'; y') là ảnh của A qua phép tịnh tiến theo vectơ v. Ta có:
x' = 1 + 3 = 4
y' = 2 - 1 = 1
Vậy A'(4; 1).
Bài 2: (Trang 68)
Cho đường thẳng d: x + y - 2 = 0. Tìm ảnh của đường thẳng d qua phép quay tâm O, góc 90°.
Giải: Gọi d' là ảnh của d qua phép quay tâm O, góc 90°. Để tìm phương trình của d', ta cần tìm hai điểm thuộc d và tìm ảnh của chúng qua phép quay. Sau đó, tìm phương trình đường thẳng đi qua hai điểm ảnh này.
Bài 3: (Trang 69)
Cho đường tròn (C): (x - 1)² + (y + 2)² = 4. Tìm ảnh của (C) qua phép đối xứng trục Ox.
Giải: Gọi (C') là ảnh của (C) qua phép đối xứng trục Ox. Tâm I(1; -2) của (C) sẽ có ảnh là I'(1; 2). Bán kính của (C') vẫn là 2. Vậy phương trình của (C') là (x - 1)² + (y - 2)² = 4.
Lưu ý quan trọng:
Trong quá trình giải bài tập, các em cần chú ý đến việc kiểm tra lại kết quả và đảm bảo rằng đáp án của mình là chính xác. Nếu gặp khó khăn, hãy tham khảo các tài liệu tham khảo hoặc hỏi ý kiến của giáo viên và bạn bè.
Tusach.vn – Đồng hành cùng bạn học Toán 11!
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác các bài tập trong SGK Toán 11 tập 1 và các tài liệu học tập khác. Hãy truy cập website của chúng tôi để được hỗ trợ tốt nhất trong quá trình học tập!
| Phép biến hình | Định nghĩa | Tính chất |
|---|---|---|
| Phép tịnh tiến | Biến mỗi điểm thành một điểm sao cho vectơ nối hai điểm bằng vectơ tịnh tiến. | Bảo toàn khoảng cách giữa hai điểm bất kỳ. |
| Phép quay | Biến mỗi điểm thành một điểm sao cho khoảng cách từ điểm đó đến tâm quay không đổi và góc tạo bởi hai đoạn thẳng nối điểm đó với tâm quay là góc quay. | Bảo toàn khoảng cách giữa hai điểm bất kỳ. |