Giải mục 1 trang 64, 65 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 64, 65 SGK Toán 11 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 64, 65 SGK Toán 11 tập 2 tại tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho quá trình học tập của các em, tusach.vn đã biên soạn bộ giải bài tập Toán 11 tập 2 đầy đủ và chính xác.
Quan sát Hình 8.28, trả lời các câu hỏi:
Hoạt động 1
Quan sát Hình 8.28, trả lời các câu hỏi:
a) Bốn cánh cửa kính 1, 2, 3, 4 (Hình 8.28) chia không gian thành bao nhiêu phần?
b) Bạn An (nữ, áo vàng) và bạn Bình (nam, áo xanh) ở phần không gian nào?
Phương pháp giải:
Quan sát hình ảnh.
Lời giải chi tiết:
a) Bốn cánh cửa kính chia không gian thành 4 phần.
b) Bạn An ở phần không gian chứa cánh cửa số 1 và 4, Bình ở phần không gian chứa cánh cửa số 1 và 2.
Hoạt động 2
Cho nhị diện \(\left[ {\alpha ,a,\beta } \right]\) và điểm O thuộc a. Vẽ mặt phẳng (P) qua O và vuông góc a. Gọi giao tuyển của (P) với các nửa mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) lần lượt là các tia Ox, Oy. Hỏi số đo góc xOy thay đổi như thế nào khi điểm O thay đổi trên a?

Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
Số đo góc xOy không thay đổi khi điểm O thay đổi trên A.
Luyện tập 1
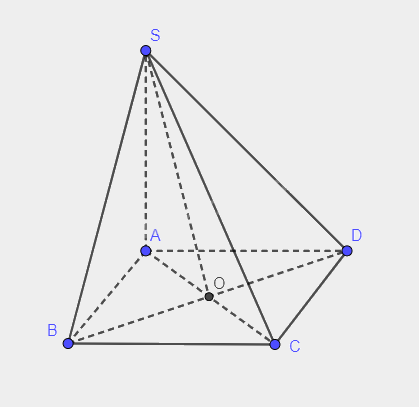
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), \(SA = \frac{{\sqrt 2 }}{2}a\). Tính số đo của các góc nhị diện \(\left[ {S,BD,A} \right]\), \(\left[ {S,BD,C} \right]\).
Phương pháp giải:
Cách tìm số đo của góc nhị diện \(\left[ {S,CD,A} \right]\):
+ Tìm giao tuyến d của (SCD) và (ACD).
+ Tìm \(a \subset \left( {SCD} \right)\) vuông góc với d. Tìm \(b \subset \left( {ACD} \right)\) vuông góc với d.
+ Tính \(\left( {a,b} \right)\).
Lời giải chi tiết:

SA vuông góc với BD (Vì SA vuông góc với (ABCD))
AC vuông với BD (Vì ABCD là hình vuông)
Nên (SAC) vuông với BD
Trong (ABCD), gọi O là giao điểm của AC và BD
Suy ra SO vuông góc với BD
Mà: AO vuông góc với BD
Suy ra góc phẳng nhị diện \(\left[ {S,BD,A} \right]\) là góc SOA
ABCD là hình vuông cạnh a nên AC bằng \(\sqrt 2 a\). Suy ra AO = \(\frac{{\sqrt 2 }}{2}a\)
\(\tan \widehat {SOA} = \,\frac{{SA}}{{AO}} = \frac{{\frac{{\sqrt 2 }}{2}a}}{{\frac{{\sqrt 2 }}{2}a}} = 1 \Rightarrow \widehat {SOA} = {45^0}\)
Ta có: SO vuông góc với BD, CO vuông góc với BD nên góc phẳng nhị diện \(\left[ {S,BD,C} \right]\) là góc SOC
\(\widehat {SOC} = {180^0} - {45^0} = {135^0}\)
Giải mục 1 trang 64, 65 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải
Mục 1 trang 64, 65 SGK Toán 11 tập 2 thuộc chương trình học về Đạo hàm. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học Toán nâng cao hơn. Mục này tập trung vào việc ôn lại các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc giải các bài toán thực tế.
Nội dung chi tiết các bài tập trong mục 1
Mục 1 bao gồm các bài tập rèn luyện kỹ năng tính đạo hàm của các hàm số đơn giản, hàm hợp, và các hàm số lượng giác. Các bài tập cũng yêu cầu học sinh vận dụng các quy tắc đạo hàm để giải các phương trình và bất phương trình.
Bài 1: Tính đạo hàm của các hàm số sau
- a) y = x3 - 2x2 + 5x - 1
- b) y = (x2 + 1)(x - 3)
- c) y = sin(2x)
Để giải các bài tập này, học sinh cần nắm vững các quy tắc đạo hàm cơ bản như đạo hàm của hàm đa thức, đạo hàm của tích hai hàm số, và đạo hàm của hàm lượng giác.
Bài 2: Tìm đạo hàm của hàm số y = f(x) tại điểm x0
Bài tập này yêu cầu học sinh áp dụng định nghĩa đạo hàm để tính đạo hàm của hàm số tại một điểm cụ thể. Học sinh cần hiểu rõ ý nghĩa của đạo hàm và cách sử dụng định nghĩa đạo hàm để giải bài toán.
Bài 3: Giải các phương trình sau
- a) f'(x) = 0
- b) f'(x) > 0
Đây là các bài tập ứng dụng đạo hàm để giải phương trình và bất phương trình. Học sinh cần hiểu rõ mối liên hệ giữa đạo hàm và tính đơn điệu của hàm số.
Phương pháp giải bài tập hiệu quả
- Nắm vững lý thuyết: Đảm bảo bạn hiểu rõ các khái niệm, định lý và quy tắc đạo hàm.
- Phân tích bài toán: Xác định rõ yêu cầu của bài toán và các thông tin đã cho.
- Chọn phương pháp giải phù hợp: Áp dụng các quy tắc đạo hàm và các kỹ năng giải toán đã học.
- Kiểm tra lại kết quả: Đảm bảo kết quả của bạn là chính xác và hợp lý.
Tại sao nên chọn tusach.vn để học Toán 11?
- Lời giải chi tiết, dễ hiểu: Chúng tôi cung cấp lời giải đầy đủ, rõ ràng, giúp bạn hiểu sâu sắc kiến thức.
- Đội ngũ giáo viên giàu kinh nghiệm: Các lời giải được biên soạn bởi các giáo viên Toán có nhiều năm kinh nghiệm.
- Cập nhật liên tục: Chúng tôi luôn cập nhật các lời giải mới nhất, đáp ứng nhu cầu học tập của bạn.
- Giao diện thân thiện, dễ sử dụng: Bạn có thể dễ dàng tìm kiếm và xem lời giải trên mọi thiết bị.
Bảng tổng hợp các công thức đạo hàm quan trọng
| Hàm số y = f(x) | Đạo hàm y' = f'(x) |
|---|---|
| C (hằng số) | 0 |
| xn | nxn-1 |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
Hy vọng với những lời giải chi tiết và phương pháp giải hiệu quả mà tusach.vn cung cấp, các em sẽ học tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi. Chúc các em thành công!