Bài 3.13 trang 79 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Bài 3.13 trang 79 SGK Toán 11 tập 1
Bài 3.13 thuộc chương trình Toán 11 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các quy tắc tính đạo hàm và khả năng áp dụng chúng vào các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Trong Vật lí, tỉ số giữa tốc độ c của ánh sáng trong chân không và của tốc độ v của ánh sáng trong một môi trường được gọi là chiết suất của môi trường đó. Chiết suất của một môi trường đồng nhất là không đổi.
Đề bài
Trong Vật lí, tỉ số giữa tốc độ c của ánh sáng trong chân không và của tốc độ v của ánh sáng trong một môi trường được gọi là chiết suất của môi trường đó. Chiết suất của một môi trường đồng nhất là không đổi. Ngày nay, với công nghệ nano, người ta tạo ra được các bản thủy tinh mà chiết suất của nó thay đổi theo một phương nào đó. Xét sự truyền của ánh sáng vào bản thủy tinh dọc theo trục Ox như Hình 3.9. Biết chiết suất của bản thủy tinh này thay đổi theo hoành độ x cho bởi: \(n\left( x \right) = \frac{a}{{a - x}}\) với \(0 \le x \le d\), trong đó \(a\) là một hằng số có giá trị lớn hơn bề dày \(d\) của bản thủy tinh.
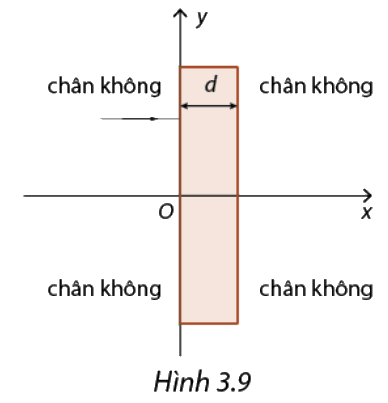
a) Chứng minh rằng tốc độ của ánh sáng cho bởi: \(v\left( x \right) = \left\{ \begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,c\,\,\,\,\,\,khi\,\,x < 0\\c\left( {1 - \frac{x}{a}} \right)\,\,\,\,\,\,khi\,\,\,0 \le x \le d\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,c\,\,\,\,\,\,khi\,\,x > d\end{array} \right.\)
b) Xét tính liên tục của hàm số \(y = v\left( x \right)\) trên \(\left( { - \infty ; + \infty } \right)\)
Phương pháp giải - Xem chi tiết
a, Ta có \(n\left( x \right) = \frac{c}{{v\left( x \right)}}\)
Trong môi trường chân không thì tốc độ của ánh sáng là c
b,Hàm số liên tục trên khoảng K nếu nó liên tục tại mọi điểm thuộc K
Hàm đa thức thì liên tục trên \(\left( { - \infty ; + \infty } \right)\)
Xét tính liên tục của hàm số tại các điểm \(x = 0,x = d\)
Hàm số liên tục tại \(x = {x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x \right) = f\left( {{x_0}} \right)\) hoặc \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải chi tiết
a, Khi \(x < 0\) hay \(x > d\) thì ánh sáng ở môi trường chân không nên \(v\left( x \right) = c\)
Khi \(0 \le x \le d\) thì \(\frac{c}{{v\left( x \right)}} = \frac{a}{{a - x}}\) vì \(n\left( x \right) = \frac{c}{{v\left( x \right)}}\), do đó \(\frac{{v\left( x \right)}}{c} = \frac{{a - x}}{a} \Leftrightarrow v\left( x \right) = c.\frac{{a - x}}{a} = c\left( {1 - \frac{x}{a}} \right)\)
b,
Tập xác định \(D = \mathbb{R}\)
Hàm số \(y = v\left( x \right)\) là hàm đa thức nên liên tục trên các khoảng \(\left( { - \infty ;0} \right)\), \(\left( {0;d} \right)\) và \(\left( {d; + \infty } \right)\)
+ Với \(x = 0 \Rightarrow v\left( 0 \right) = c\)
\(\mathop {\lim }\limits_{x \to {0^ - }} v\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} c = c;\,\,\mathop {\lim }\limits_{x \to {0^ + }} v\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} c\left( {1 - \frac{x}{a}} \right) = c\left( {1 - \frac{0}{a}} \right) = c\)
Suy ra \(\mathop {\lim }\limits_{x \to {0^ + }} v\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} v\left( x \right) = v\left( 0 \right)\) nên hàm số \(v\left( x \right)\) liên tục tại \(x = 0\)
+ Với \(x = d \Rightarrow v\left( d \right) = c\left( {1 - \frac{d}{a}} \right)\)
\(\mathop {\lim }\limits_{x \to {d^ - }} v\left( x \right) = \mathop {\lim }\limits_{x \to {d^ - }} c\left( {1 - \frac{x}{a}} \right) = c\left( {1 - \frac{d}{a}} \right);\,\,\mathop {\lim }\limits_{x \to {d^ + }} v\left( x \right) = \mathop {\lim }\limits_{x \to {d^ + }} c = c\)
Suy ra \(\mathop {\lim }\limits_{x \to {d^ - }} v\left( x \right) \ne \,\mathop {\lim }\limits_{x \to {d^ + }} v\left( x \right)\) nên hàm số \(y = v\left( x \right)\) không liên tục tại điểm \(x = d\)
Vậy hàm số \(y = v\left( x \right)\) không liên tục trên \(\left( { - \infty ; + \infty } \right)\). Hàm số \(y = v\left( x \right)\) liên tục trên các khoảng \(\left( { - \infty ;d} \right)\) và \(\left( {d; + \infty } \right)\)
Bài 3.13 Trang 79 SGK Toán 11 Tập 1: Giải Chi Tiết và Hướng Dẫn
Bài 3.13 trang 79 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 3.13 thường yêu cầu học sinh tính đạo hàm của một hàm số hoặc giải một phương trình liên quan đến đạo hàm. Ví dụ, bài tập có thể yêu cầu:
- Tính đạo hàm của hàm số f(x) = x3 - 2x2 + 5x - 1.
- Tìm đạo hàm của hàm số y = sin(2x) + cos(x).
- Giải phương trình f'(x) = 0.
Phương pháp giải
Để giải bài 3.13, học sinh cần nắm vững các quy tắc tính đạo hàm sau:
- Đạo hàm của một hằng số bằng 0.
- Đạo hàm của xn bằng nxn-1.
- Đạo hàm của sin(x) bằng cos(x).
- Đạo hàm của cos(x) bằng -sin(x).
- Quy tắc chuỗi: Nếu y = f(g(x)), thì y' = f'(g(x)) * g'(x).
Lời giải chi tiết (Ví dụ)
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x3 - 2x2 + 5x - 1.
Áp dụng các quy tắc đạo hàm, ta có:
f'(x) = 3x2 - 4x + 5
Ví dụ 2: Tìm đạo hàm của hàm số y = sin(2x) + cos(x).
Áp dụng quy tắc chuỗi và các quy tắc đạo hàm cơ bản, ta có:
y' = cos(2x) * 2 - sin(x) = 2cos(2x) - sin(x)
Mẹo giải nhanh
Để giải nhanh các bài tập về đạo hàm, học sinh nên:
- Nắm vững các quy tắc đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
Bài tập tương tự
Để củng cố kiến thức, học sinh có thể làm thêm các bài tập tương tự sau:
- Tính đạo hàm của hàm số g(x) = 4x2 + 3x - 2.
- Tìm đạo hàm của hàm số h(x) = tan(x) + cot(x).
- Giải phương trình f'(x) = 6x - 2.
Kết luận
Bài 3.13 trang 79 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng của nó. Bằng cách nắm vững các quy tắc đạo hàm và luyện tập thường xuyên, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.
Chúc các em học tốt!
| Hàm số | Đạo hàm |
|---|---|
| f(x) = x3 | f'(x) = 3x2 |
| y = sin(x) | y' = cos(x) |