Giải mục 3 trang 68, 69 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 68, 69 SGK Toán 11 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 68, 69 SGK Toán 11 tập 2 tại tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho quá trình học tập của các em, tusach.vn đã biên soạn và trình bày lời giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng.
Quan sát Hình 8.41.
Hoạt động 7
Quan sát Hình 8.41.
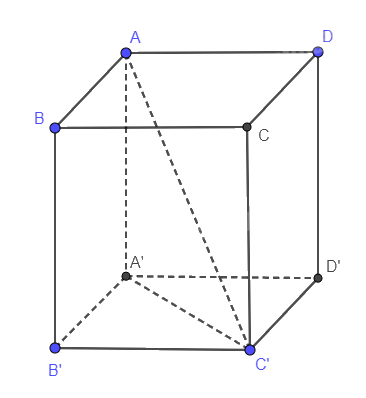
Xét hình lăng trụ (3). Biết rằng lăng trụ này có hai mặt bên chung cạnh AA’ là hai hình chữ nhật.
a) Cạnh AA' có vuông góc với mặt đáy không? Vì sao?
b) Các mặt bên còn lại là những hình gì? Vì sao?
Phương pháp giải:
a) Nếu một đường thẳng vuông góc với 2 đường thẳng cắt nhau cùng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
b) Hình lăng trụ có các cạnh bên song song với nhau và các mặt bên là hình bình hành.
Lời giải chi tiết:
a) Vì AA’ vuông góc với AB và AE nên AA’ vuông góc với (ABCDE).
b) Hình lăng trụ có các cạnh bên song song với nhau và các mặt bên là hình bình hành. Mà AA’ vuông góc với đáy nên các cạnh bên còn lại cũng vuông góc với đáy. Suy ra các mặt bên là hình chữ nhật.
Luyện tập 5
Tính độ dài đường chéo của hình hộp chữ nhật ABCD.A’B’C’D’ biết AA’ = 6a, AD = 3a, AB = 2a.
Phương pháp giải:
Áp dụng định lý Py-ta-go để tính A’C’. Từ đó tính AC.
Lời giải chi tiết:

ABCD.A’B’C’D’ là hình hộp chữ nhật nên A’B’ = AB = 2a, B’C’ = BC = 3a
Xét tam giác A’B’C’ vuông tại B’ có:
\(A'C = \sqrt {A'B{'^2} + B'C{'^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {3a} \right)}^2}} = \sqrt {13} a\)
Xét tam giác AA’C vuông tại A’ có:
\(AC = \sqrt {AA{'^2} + A'{C^2}} = \sqrt {{{\left( {6a} \right)}^2} + {{\left( {\sqrt {13} a} \right)}^2}} = 7a\)
Giải mục 3 trang 68, 69 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải
Mục 3 trang 68, 69 SGK Toán 11 tập 2 tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Đây là một phần quan trọng trong chương trình Toán 11, đòi hỏi học sinh nắm vững các kiến thức về hàm số lượng giác, đồ thị hàm số lượng giác, và các phương trình lượng giác cơ bản.
Nội dung chính của Mục 3
- Ôn tập lý thuyết: Nhắc lại các định nghĩa, tính chất, và công thức liên quan đến hàm số lượng giác (sin, cos, tan, cot).
- Bài tập vận dụng: Các bài tập trong mục này yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán về hàm số lượng giác, tìm tập xác định, tập giá trị, xét tính đơn điệu, và vẽ đồ thị hàm số.
- Bài tập nâng cao: Một số bài tập đòi hỏi học sinh phải có khả năng tư duy và sáng tạo để giải quyết.
Giải chi tiết các bài tập trong Mục 3
Bài 1: (Trang 68)
Bài 1 yêu cầu học sinh xác định tập xác định của hàm số. Để giải bài này, cần nhớ lại điều kiện xác định của các hàm số lượng giác. Ví dụ, hàm số y = tan(x) xác định khi và chỉ khi x ≠ π/2 + kπ (k ∈ Z).
Bài 2: (Trang 68)
Bài 2 yêu cầu học sinh tìm tập giá trị của hàm số. Để giải bài này, cần xét khoảng giá trị của hàm số lượng giác. Ví dụ, -1 ≤ sin(x) ≤ 1 và -1 ≤ cos(x) ≤ 1.
Bài 3: (Trang 69)
Bài 3 yêu cầu học sinh xét tính đơn điệu của hàm số. Để giải bài này, cần sử dụng đạo hàm của hàm số lượng giác. Ví dụ, đạo hàm của sin(x) là cos(x) và đạo hàm của cos(x) là -sin(x).
Bài 4: (Trang 69)
Bài 4 yêu cầu học sinh vẽ đồ thị hàm số. Để vẽ đồ thị hàm số, cần xác định các điểm đặc biệt (điểm cực đại, điểm cực tiểu, điểm uốn) và vẽ đồ thị qua các điểm này.
Phương pháp giải bài tập Hàm số lượng giác hiệu quả
- Nắm vững lý thuyết: Đây là nền tảng quan trọng để giải quyết mọi bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị có thể giúp bạn giải quyết các bài tập một cách nhanh chóng và chính xác.
- Tham khảo các nguồn tài liệu: Sách giáo khoa, sách bài tập, các trang web học tập trực tuyến có thể cung cấp cho bạn thêm kiến thức và phương pháp giải bài tập.
Lời khuyên khi học tập
Học Toán 11 đòi hỏi sự kiên trì và nỗ lực. Hãy dành thời gian ôn tập lý thuyết, làm bài tập, và tìm kiếm sự giúp đỡ khi gặp khó khăn. Đừng ngại đặt câu hỏi cho giáo viên hoặc bạn bè. Chúc các em học tập tốt!
| Bài tập | Mức độ khó | Gợi ý giải |
|---|---|---|
| Bài 1 | Dễ | Xác định điều kiện xác định của hàm số lượng giác. |
| Bài 2 | Trung bình | Tìm khoảng giá trị của hàm số lượng giác. |
| Bài 3 | Khó | Sử dụng đạo hàm để xét tính đơn điệu. |