Lý Thuyết Hàm Số Liên Tục - SGK Toán 11

Lý thuyết Hàm số liên tục - SGK Toán 11 Cùng khám phá

Lý thuyết Hàm số liên tục - SGK Toán 11

Hàm số liên tục là một khái niệm nền tảng quan trọng trong chương trình Toán 11. Việc nắm vững lý thuyết này không chỉ giúp bạn hiểu sâu hơn về tính chất của hàm số mà còn là bước đệm quan trọng cho các kiến thức nâng cao hơn trong chương trình học.

Tusach.vn xin giới thiệu tài liệu Lý thuyết Hàm số liên tục - SGK Toán 11, được trình bày một cách dễ hiểu, logic, kèm theo các ví dụ minh họa và bài tập vận dụng để bạn có thể tự học hiệu quả.

I. Hàm số liên tục tại một điểm và liên tục trên một khoảng

I. Hàm số liên tục tại một điểm và liên tục trên một khoảng

1. Hàm số liên tục tại 1 điểm

Cho hàm \(y = f(x)\) xác định trên khoảng K, \({x_0} \in K\). Hàm số \(f(x)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\).

Hàm số không liên tục tại \({x_0}\) được gọi là gián đoạn tại điểm đó.

2. Hàm số liên tục trên một khoảng

- Hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;b} \right)\)

Hàm số \(y = f(x)\) được gọi là liên tục trên khoảng \(\left( {a;b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này.

- Hàm số \(y = f(x)\) được gọi là liên tục trên đoạn \(\left[ {a;b} \right]\) nếu nó liên tục trên khoảng \(\left( {a;b} \right)\) và \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a),\mathop {\lim }\limits_{x \to {b^ - }} f(x) = f(b)\).

* Nhận xét:

- Đồ thị hàm số liên tục trên một khoảng, đoạn là “đường liền” trên khoảng, đoạn đó.

- Nếu hàm số\(y = f(x)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f(a).f(b) < 0\)thì phương trình \(f(x) = 0\)có ít nhất một nghiệm trên khoảng \(\left( {a;b} \right)\).

II. Một số định lí cơ bản

1. Định lí 1

- Hàm số đa thức và hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}},y = c{\rm{osx}}\)liên tục trên \(\mathbb{R}\).

- Các hàm số \(y = \tan {\rm{x}},y = c{\rm{otx,}}y = \sqrt x \) và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác định của chúng.

2. Định lí 2

Giả sử hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục tại điểm \({x_0}\). Khi đó:

a, Các hàm số \(y = f(x) \pm g(x)\) và \(y = f(x).g(x)\) liên tục tại điểm \({x_0}\).

b, Hàm số \(y = \frac{{f(x)}}{{g(x)}}\) liên tục tại điểm \({x_0}\) nếu \(g({x_0}) \ne 0\).

c, Hàm số \(y = f(x)\) liên tục trên khoảng K và \(f(x) \ge 0,\forall x \in K\). Khi đó hàm số \(y = \sqrt {f(x)} \) liên tục trên K.

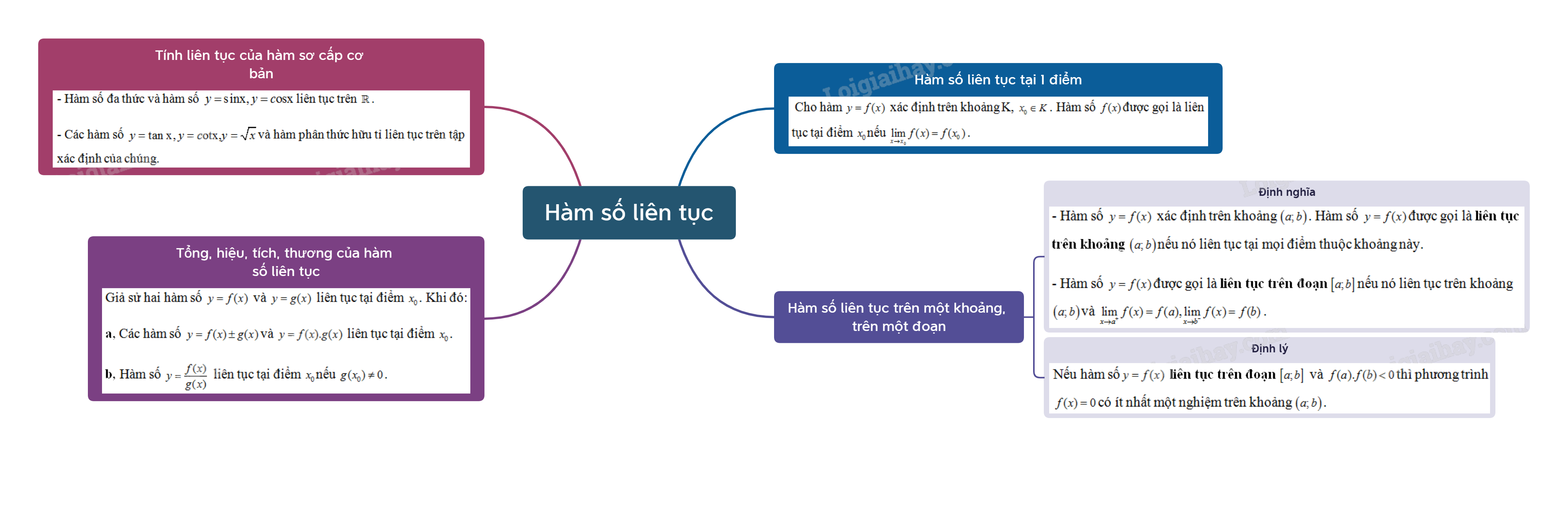
Lý thuyết Hàm số liên tục - SGK Toán 11 Cùng khám phá 1

Lý Thuyết Hàm Số Liên Tục - SGK Toán 11: Tổng Quan và Ứng Dụng

Hàm số liên tục là một trong những khái niệm cơ bản và quan trọng nhất trong giải tích. Nó đóng vai trò then chốt trong việc nghiên cứu tính chất của hàm số, giải các bài toán về giới hạn, đạo hàm và tích phân. Bài viết này sẽ cung cấp một cái nhìn tổng quan về lý thuyết hàm số liên tục theo chương trình SGK Toán 11, bao gồm định nghĩa, điều kiện liên tục, các tính chất và ứng dụng của nó.

1. Định Nghĩa Hàm Số Liên Tục

Một hàm số f(x) được gọi là liên tục tại điểm x₀ nếu thỏa mãn ba điều kiện sau:

Hàm số f(x) xác định tại x₀, tức là f(x₀) có nghĩa.
Tồn tại giới hạn của f(x) khi x tiến tới x₀, ký hiệu là lim_x→x₀f(x).
Giá trị của hàm số tại x₀ bằng giới hạn của nó tại x₀, tức là f(x₀) = lim_x→x₀f(x).

Hàm số f(x) được gọi là liên tục trên khoảng (a, b) nếu nó liên tục tại mọi điểm trong khoảng đó.

2. Điều Kiện Liên Tục của Hàm Số

Để kiểm tra tính liên tục của một hàm số, ta có thể sử dụng các điều kiện sau:

Hàm đa thức: Mọi hàm đa thức đều liên tục trên tập số thực ℝ.
Hàm phân thức: Hàm phân thức f(x) = P(x) / Q(x) liên tục trên tập hợp các điểm mà Q(x) ≠ 0.
Hàm căn thức: Hàm căn thức √f(x) liên tục trên tập hợp các điểm mà f(x) ≥ 0.
Hàm lượng giác: Các hàm lượng giác sin(x), cos(x) liên tục trên tập số thực ℝ.

3. Các Tính Chất của Hàm Số Liên Tục

Hàm số liên tục có một số tính chất quan trọng sau:

Tổng, hiệu, tích của các hàm số liên tục là một hàm số liên tục.
Thương của hai hàm số liên tục (với mẫu khác 0) là một hàm số liên tục.
Hàm hợp của các hàm số liên tục là một hàm số liên tục.

4. Ứng Dụng của Lý Thuyết Hàm Số Liên Tục

Lý thuyết hàm số liên tục có nhiều ứng dụng trong thực tế, bao gồm:

Giải các bài toán về giới hạn: Tính giới hạn của hàm số bằng cách sử dụng tính liên tục.
Nghiên cứu tính chất của hàm số: Xác định khoảng liên tục, khoảng gián đoạn của hàm số.
Ứng dụng trong vật lý: Mô tả các hiện tượng vật lý liên tục, chẳng hạn như chuyển động đều.
Ứng dụng trong kinh tế: Phân tích các hàm số chi phí, doanh thu, lợi nhuận.

5. Bài Tập Vận Dụng

Để củng cố kiến thức về lý thuyết hàm số liên tục, bạn có thể thực hành các bài tập sau:

Bài tập	Nội dung
1	Kiểm tra tính liên tục của hàm số f(x) = (x² - 1) / (x - 1) tại x = 1.
2	Tìm khoảng liên tục của hàm số f(x) = √(x - 2).
3	Chứng minh hàm số f(x) = x³ + 2x - 1 liên tục trên ℝ.

Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn toàn diện về lý thuyết hàm số liên tục - SGK Toán 11. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng nó vào giải các bài toán thực tế.

Truy cập tusach.vn để xem thêm nhiều tài liệu học tập Toán 11 hữu ích khác!