Giải mục 3 trang 83 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 83 SGK Toán 11 tập 2 - Cùng khám phá
Chào mừng bạn đến với lời giải chi tiết bài tập mục 3 trang 83 SGK Toán 11 tập 2 trên tusach.vn. Bài viết này sẽ cung cấp cho bạn đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để bạn hiểu sâu hơn về kiến thức Toán học.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp bạn học Toán 11 một cách hiệu quả nhất.
Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’ cạnh bên bằng 8a
Luyện tập 3
Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’ cạnh bên bằng 8a, cạnh đáy lớn bằng 5a, cạnh đáy nhỏ bằng a. Tính thể tích hình chóp cụt đều này.
Phương pháp giải:
Áp dụng công thức tính thể tích khối chóp cụt đều có chiều cao h và diện tích 2 đáy lần lượt là S và S’: \(V = \frac{1}{3}h\left( {S + S' + \sqrt {SS'} } \right)\)
Lời giải chi tiết:
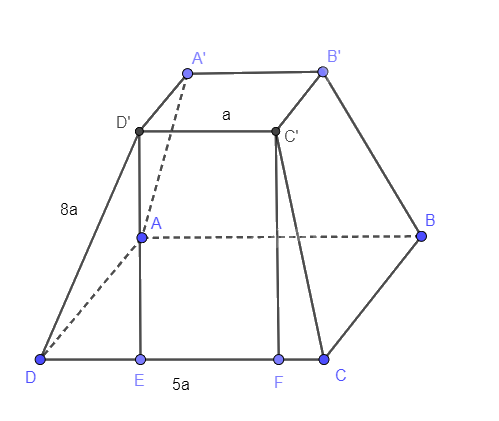
Kẻ D’E và D’F vuông góc với CD nên D’E // D’F
Mà C’D’ // EF nên D’C’FE là hình bình hành. Suy ra EF = D’C’ = a
\( \Rightarrow DE + CF = DC - EF = 5a - a = 4a\)\( \Rightarrow DE = CF = 2a\)
\(D'E = \sqrt {D'{B^2} - D{E^2}} = \sqrt {{{\left( {8a} \right)}^2} - {{\left( {2a} \right)}^2}} = 2\sqrt {15} a\)
\({S_{ABCD}} = {\left( {5a} \right)^2} = 25{a^2}\)
\({S_{A'B'C'D'}} = {a^2}\)
\( \Rightarrow V = \frac{1}{3}.2\sqrt {15} a.\left( {25{a^2} + {a^2} + \sqrt {25{a^2}.{a^2}} } \right) = \frac{{62\sqrt {15} }}{3}{a^3}\)
Vận dụng
Bạn An muốn làm các viên nước đá có dạng khối chóp cụt tứ giác đều có đáy lớn bằng 3 cm, đáy nhỏ bằng 1,5 cm và cao 3 cm bằng cách dùng khay đá, mỗi khay sẽ tạo được 6 viên đá. Hỏi bạn An cần ít nhất bao nhiêu khay để chứa đồng thời 2 lít nước?
Phương pháp giải:
Áp dụng công thức tính thể tích khối chóp cụt đều có chiều cao h và diện tích 2 đáy lần lượt là S và S’: \(V = \frac{1}{3}h\left( {S + S' + \sqrt {SS'} } \right)\) để tính thể tích mỗi viên nước đá.
Lời giải chi tiết:
2 lít = 2000 cm3
\(V = \frac{1}{3}.3.\left( {{3^2} + 1,{5^2} + \sqrt {{3^2}.1,{5^2}} } \right) = 15,75\) (cm3)
Từ 2 lít nước có thể tạo ra số viên đá là: \(2000:15,75 \approx 127\) (viên)
Ta có: \(\frac{{127}}{6} \approx 21,2\)
Vậy cần ít nhất 22 khay nước để chứa đồng thời 2 lít nước.
Giải mục 3 trang 83 SGK Toán 11 tập 2 - Cùng khám phá: Tổng quan và Phương pháp
Mục 3 trang 83 SGK Toán 11 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các dạng bài tập tính đạo hàm, ứng dụng đạo hàm để khảo sát hàm số và giải các bài toán liên quan đến tối ưu hóa. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Nội dung chi tiết Giải mục 3 trang 83 SGK Toán 11 tập 2
Để giúp các em học sinh hiểu rõ hơn về nội dung bài học, chúng ta sẽ cùng nhau đi sâu vào từng bài tập cụ thể trong mục 3 trang 83 SGK Toán 11 tập 2.
Bài 1: Tính đạo hàm của các hàm số sau
Bài tập này yêu cầu các em áp dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của các hàm số cho trước. Cần chú ý đến các quy tắc như đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp.
- Ví dụ: Tính đạo hàm của hàm số y = x3 + 2x2 - 5x + 1.
- Lời giải: y' = 3x2 + 4x - 5
Bài 2: Tìm đạo hàm cấp hai của hàm số y = sin(2x)
Bài tập này yêu cầu các em tính đạo hàm bậc hai của hàm số lượng giác. Cần nhớ công thức đạo hàm của hàm sin và quy tắc tính đạo hàm cấp hai.
y' = 2cos(2x)
y'' = -4sin(2x)
Bài 3: Khảo sát hàm số y = x3 - 3x2 + 2
Bài tập này yêu cầu các em khảo sát hàm số bằng cách tìm các điểm cực trị, điểm uốn và vẽ đồ thị hàm số. Cần sử dụng đạo hàm bậc nhất và đạo hàm bậc hai để xác định các điểm này.
- Bước 1: Tính đạo hàm bậc nhất y' = 3x2 - 6x.
- Bước 2: Giải phương trình y' = 0 để tìm các điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2.
- Bước 3: Tính đạo hàm bậc hai y'' = 6x - 6.
- Bước 4: Xác định loại điểm cực trị bằng cách xét dấu y'' tại các điểm cực trị.
Lưu ý khi giải bài tập mục 3 trang 83 SGK Toán 11 tập 2
- Nắm vững các quy tắc tính đạo hàm.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra kết quả.
- Tham khảo các tài liệu tham khảo khác để hiểu sâu hơn về kiến thức.
Bảng tổng hợp các công thức đạo hàm quan trọng
| Hàm số | Đạo hàm |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sin(x) | y' = cos(x) |
| y = cos(x) | y' = -sin(x) |
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 3 trang 83 SGK Toán 11 tập 2. Chúc các em học tập tốt!
Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại để lại bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ bạn.