Giải mục 2 trang 62, 63, 64 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 62, 63, 64 SGK Toán 11 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 62, 63, 64 SGK Toán 11 tập 1. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập.
Bài viết này sẽ cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải chi tiết, giúp các em tự tin hơn khi làm bài tập về nhà.
Cho dãy số chính phương (({u_n})) với ({u_n} = {n^2})
Hoạt động 5
Cho dãy số chính phương (\({u_n}\)) với \({u_n} = {n^2}\)
a, Viết các số hạng tương ứng của dãy số (\({u_n}\)) trong bảng sau:
b, Từ kết quả thu được, nhận xét về giá trị \({u_n}\) khi n tăng lên vô hạn.
c, Từ số hạng thứ mấy thì mọi số hạng \({u_n}\) đều thỏa mãn \({u_n} > 10000000000\)?
Phương pháp giải:
a, Thay các giá trị của n=1,2,3,… để được các giá trị của \({u_n}\) tương ứng.
b, Khi n tăng vô hạn \({u_n} = {n^2}\) cũng tăng lên vô hạn
c, Giá trị 10000000000 ứng với \({u_{100000}}\)
Với các giá trị n>100000 thỏa mãn \({u_n} > 10000000000\)
Lời giải chi tiết:
a, Ta có: \({u_1} = {1^2} = 1;{u_2} = {2^2} = 4;{u_3} = {3^2} = 9;{u_4} = {4^2} = 16\)
\({u_5} = {5^2} = 25;{u_6} = {6^2} = 36;{u_7} = {7^2} = 49;{u_8} = {8^2} = 64\)
\({u_{1000}} = {1000^2} = 1000000\)

b, Từ kết quả câu a ta thấy khi n tăng lên vô hạn thì giá trị \({u_n} = {n^2}\) cũng tăng lên vô hạn.
c, Ta có; \({u_{100000}} = 10000000000\).
Để \({u_n} > 10000000000\) thì n > 100000.
Luyện tập 5
Tìm \(\lim ({2^n}{.3^n}{.4^n})\).
Phương pháp giải:
Áp dụng lim \({q^n} = + \infty \) với q > 1.
Lời giải chi tiết:
Ta có: \(\lim ({2^n}{.3^n}{.4^n}) = \lim ({12^n}) = + \infty \).
Vận dụng
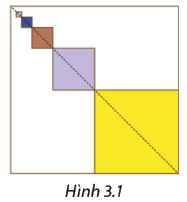
Một nhà thầu nhận được hợp đồng sơn màu trang trí một bức tường hình vuông màu trắng kích thước 4m x 4m của một trường mẫu giáo. Hai điều kiện của hợp đồng như sau:
a, Các hình vuông cần sơn màu như hình 3.1. Hình vuông lớn nhất có diện tích bằng một phần tư diện tích bức tường được sơn màu tùy ý khác màu trắng. Mỗi hình vuông tiếp theo có diện tích bằng một phần tư diện tích hình vuông trước nó, được sơn màu khác với hình vuông trước đó và màu trắng;
b, Một phần ba bức tường phải được sơn màu.
Sau khi xem các điều kiện của hợp đồng thì nhà thầu từ chối vì cho rằng không thể thực hiện theo yêu cầu của nhà trường. Hãy giải thích lí do vì sao họ từ chối hợp đồng.

Phương pháp giải:
Diện tích các hình vuông cần sơn là một cấp số nhân lùi vô hạn với q=\(\frac{1}{4}\).
Tổng diện tích các hình vuông cần sơn là tổng của cấp số nhân lùi vô hạn với \({u_1} = 4\) và q=\(\frac{1}{4}\).
Áp dụng công thức tính tổng cấp số nhân lùi vô hạn :
lim\({S_n} = \)\( = \frac{{{u_1}}}{{1 - q}}\).
Lời giải chi tiết:
Vì diện tích hình vuông sau bằng một phần tư diện tích hình vuông trước đó nên diện tích các hình vuông cần sơn là một cấp số nhân lùi vô hạn với công bội q=\(\frac{1}{4}\).
Diện tích hình vuông lớn nhất bằng một phần tư diện tích bức tường nên diện tích hình vuông thứ nhất là: \({u_1} = \frac{1}{4}.4.4 = 4\)(\({m^2}\)).
Tổng diện tích các hình vuông cần được sơn là một cấp số nhân lùi vô hạn với \({u_1} = 4\) và q=\(\frac{1}{4}\) ta có:
S= \({u_1} + {u_2} + ... + {u_n} + ...\)=lim\({S_n} = \)\( = \frac{{{u_1}}}{{1 - q}} = \frac{4}{{1 - \frac{1}{4}}} = \frac{4}{{\frac{3}{4}}} = \frac{{16}}{3}\).
\( \Rightarrow \)lim \({S_n}\) bằng một phần ba diện tích của bức tường
Như vậy, không tìm đươc giá trị của n để thỏa mãn điều kiện b của nhà trường. Do đó, nhà thầu từ chối hợp đồng.
Giải mục 2 trang 62, 63, 64 SGK Toán 11 tập 1: Tổng quan và Phương pháp giải
Mục 2 của SGK Toán 11 tập 1 thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 11.
Nội dung chính của Mục 2
- Phép tịnh tiến: Định nghĩa, tính chất, và ứng dụng trong việc giải các bài toán hình học.
- Phép quay: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép quay.
- Phép đối xứng trục: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép đối xứng trục.
- Phép đối xứng tâm: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép đối xứng tâm.
Giải chi tiết các bài tập trang 62, 63, 64
Bài 1: (Trang 62)
Bài tập này thường yêu cầu xác định ảnh của một điểm hoặc một hình qua một phép biến hình cho trước. Để giải bài tập này, các em cần nắm vững định nghĩa và tính chất của phép biến hình đó. Ví dụ, nếu bài tập yêu cầu tìm ảnh của điểm A(x0, y0) qua phép tịnh tiến theo vectơ v = (a, b), thì ảnh của A là điểm A'(x0 + a, y0 + b).
Bài 2: (Trang 63)
Bài tập này có thể yêu cầu chứng minh một tính chất liên quan đến phép biến hình. Để giải bài tập này, các em cần sử dụng các định lý và tính chất đã học trong sách giáo khoa. Ví dụ, để chứng minh hai đường thẳng song song, các em có thể sử dụng tính chất của phép tịnh tiến hoặc phép quay.
Bài 3: (Trang 64)
Bài tập này thường là bài toán ứng dụng, yêu cầu các em sử dụng kiến thức về phép biến hình để giải quyết một vấn đề thực tế. Để giải bài tập này, các em cần phân tích đề bài một cách cẩn thận và tìm ra mối liên hệ giữa các yếu tố của bài toán với các phép biến hình đã học.
Mẹo giải bài tập hiệu quả
- Nắm vững định nghĩa và tính chất: Đây là nền tảng quan trọng để giải quyết mọi bài tập.
- Vẽ hình: Vẽ hình giúp các em hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng các công thức và định lý: Áp dụng các công thức và định lý đã học để giải bài tập một cách chính xác.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Bảng tổng hợp công thức quan trọng
| Phép biến hình | Công thức |
|---|---|
| Tịnh tiến | A'(x0 + a, y0 + b) |
| Quay | (Công thức quay phức tạp hơn, tùy thuộc vào tâm quay và góc quay) |
| Đối xứng trục | (Công thức đối xứng trục phức tạp hơn, tùy thuộc vào trục đối xứng) |
| Đối xứng tâm | A'(2x0 - a, 2y0 - b) |
Hy vọng với những hướng dẫn chi tiết này, các em sẽ tự tin hơn khi giải các bài tập mục 2 trang 62, 63, 64 SGK Toán 11 tập 1. Chúc các em học tốt!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.