Bài 8.31 trang 83 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Bài 8.31 trang 83 SGK Toán 11 tập 2
Bài 8.31 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các công thức đạo hàm cơ bản và kỹ năng giải quyết bài toán liên quan đến ứng dụng của đạo hàm.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình chữ nhật, AB = 3a và AD = 4a.
Đề bài
Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình chữ nhật, AB = 3a và AD = 4a. Hình chiếu vuông góc của A’ trên mặt phẳng (ABCD) là trung điểm của AD và AA’ = 4a. Tính thể tích khối hộp này.
Phương pháp giải - Xem chi tiết
Công thức tính thể tích hình hộp: V = S.h với S là diện tích đáy, h là chiều cao.
Lời giải chi tiết
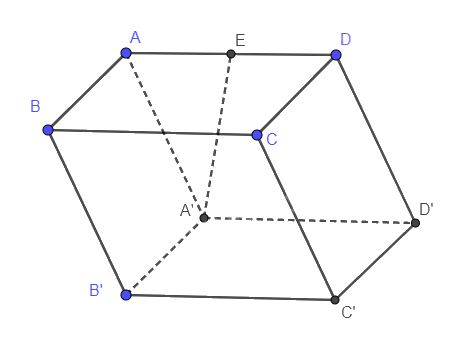
Gọi E là trung điểm của AD nên AE = 2a
\(A'E = \sqrt {AA{'^2} - A{E^2}} = \sqrt {{{\left( {4a} \right)}^2} - {{\left( {2a} \right)}^2}} = 2\sqrt 3 a\)
\(V = S.h = AB.AD.A'E = 3a.4a.2\sqrt 3 a = 24\sqrt 3 {a^3}\)
Bài 8.31 Trang 83 SGK Toán 11 Tập 2: Giải Chi Tiết và Phân Tích
Bài 8.31 trang 83 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Bài tập này thường liên quan đến việc tìm đạo hàm của hàm số, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến, và tìm cực trị của hàm số.
Nội Dung Bài 8.31
Thông thường, bài 8.31 sẽ yêu cầu học sinh thực hiện các bước sau:
- Tính đạo hàm f'(x) của hàm số đã cho.
- Tìm tập xác định của hàm số.
- Giải phương trình f'(x) = 0 để tìm các điểm cực trị.
- Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến và cực trị của hàm số.
- Kết luận về tính đơn điệu và cực trị của hàm số.
Ví Dụ Minh Họa
Giả sử bài 8.31 yêu cầu xét hàm số f(x) = x3 - 3x2 + 2.
- Tính đạo hàm: f'(x) = 3x2 - 6x
- Giải phương trình f'(x) = 0: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Lập bảng biến thiên:
x -∞ 0 2 +∞ f'(x) + - + f(x) Đồng biến Nghịch biến Đồng biến - Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 với giá trị f(0) = 2 và đạt cực tiểu tại x = 2 với giá trị f(2) = -2.
Mẹo Giải Bài Tập Đạo Hàm
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng bảng biến thiên để trực quan hóa sự thay đổi của hàm số.
- Kiểm tra lại kết quả sau khi giải xong.
Tại Sao Nên Chọn tusach.vn?
tusach.vn cung cấp:
- Lời giải chi tiết, dễ hiểu, được trình bày rõ ràng.
- Đội ngũ giáo viên giàu kinh nghiệm, luôn sẵn sàng hỗ trợ học sinh.
- Cập nhật liên tục các bài giải mới nhất.
- Giao diện thân thiện, dễ sử dụng.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và giải quyết mọi khó khăn trong quá trình học Toán 11!