Giải mục 1 trang 24, 25 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 24, 25 SGK Toán 11 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 24, 25 SGK Toán 11 tập 2. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {\log _a}x\) và đường thẳng y = b.
Hoạt động 1
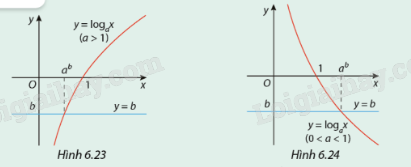
Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {\log _a}x\) và đường thẳng y = b.
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm \({\log _a}x = b\)
Phương trình luôn có nghiệm duy nhất \(x = {a^b}\forall b\)
Luyện tập 1
Giải các phương trình
a) \({\log _2}\left( {2x + 6} \right) + {\log _2}x = 3\)
b) \(\log x = \log \left( {{x^2} + x - 1} \right)\)
Phương pháp giải:
\(b = {\log _a}A \Leftrightarrow {\log _a}A = {\log _a}B \Leftrightarrow \left\{ \begin{array}{l}A > 0\\B > 0\\A = B\end{array} \right.\)
Lời giải chi tiết:
a) Điều kiện: \(\left\{ \begin{array}{l}2x + 6 > 0\\x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 3\\x > 0\end{array} \right. \Leftrightarrow x > 0\)
\(\begin{array}{l}{\log _2}\left( {2x + 6} \right) + {\log _2}x = 3\\ \Leftrightarrow {\log _2}\left[ {\left( {2x + 6} \right)x} \right] = {\log _2}8\\ \Leftrightarrow 2{x^2} + 6x = 8\\ \Leftrightarrow 2{x^2} + 6x - 8 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {{\rm{TM}}} \right)\\x = - 4\left( {\rm{L}} \right)\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm là x = 1
b) Điều kiện: x > 0
\(\begin{array}{l}\log x = \log \left( {{x^2} + x - 1} \right)\\ \Leftrightarrow x = {x^2} + x - 1\\ \Leftrightarrow {x^2} - 1 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {{\rm{TM}}} \right)\\x = - 1\left( {\rm{L}} \right)\end{array} \right.\end{array}\)
Vậy phương trình có tập nghiệm là x = 1
Giải mục 1 trang 24, 25 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải
Mục 1 trang 24, 25 SGK Toán 11 tập 2 thường xoay quanh các kiến thức về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 11.
Nội dung chi tiết Giải mục 1 trang 24, 25
Để giúp các em hiểu rõ hơn về nội dung này, chúng ta sẽ đi qua từng bài tập cụ thể:
Bài 1: Tính đạo hàm của các hàm số sau
- f(x) = x3 - 2x2 + 5x - 1
- g(x) = sin(x) + cos(x)
- h(x) = ex + ln(x)
Hướng dẫn giải:
- Áp dụng quy tắc đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
- Sử dụng các công thức đạo hàm cơ bản: (xn)' = nxn-1, (sin(x))' = cos(x), (cos(x))' = -sin(x), (ex)' = ex, (ln(x))' = 1/x.
Bài 2: Tìm đạo hàm cấp hai của hàm số f(x) = x4 - 3x2 + 2
Hướng dẫn giải:
Đạo hàm cấp hai là đạo hàm của đạo hàm cấp một. Đầu tiên, tính f'(x), sau đó tính đạo hàm của f'(x) để được f''(x).
Bài 3: Xác định khoảng đơn điệu của hàm số y = x3 - 6x2 + 9x + 1
Hướng dẫn giải:
- Tính đạo hàm y' của hàm số.
- Giải phương trình y' = 0 để tìm các điểm cực trị.
- Lập bảng xét dấu y' để xác định khoảng đồng biến và nghịch biến của hàm số.
Lưu ý quan trọng khi giải bài tập về đạo hàm
- Nắm vững các quy tắc tính đạo hàm.
- Sử dụng thành thạo các công thức đạo hàm cơ bản.
- Kiểm tra lại kết quả sau khi tính toán.
- Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.
Ứng dụng của đạo hàm trong thực tế
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
- Tính vận tốc và gia tốc trong vật lý.
- Tìm cực trị của hàm số trong kinh tế.
- Xây dựng các mô hình toán học trong khoa học kỹ thuật.
Tài liệu tham khảo thêm
Để hiểu sâu hơn về đạo hàm và các ứng dụng của nó, các em có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Toán 11 tập 2.
- Sách bài tập Toán 11 tập 2.
- Các trang web học Toán trực tuyến uy tín.
Kết luận
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập về đạo hàm trong SGK Toán 11 tập 2. Chúc các em học tập tốt!