Lý thuyết Phương trình, bất phương trình mũ và lôgarit - Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý Thuyết Phương Trình, Bất Phương Trình Mũ và Lôgarit - Toán 11 Chân Trời Sáng Tạo
Chào mừng bạn đến với chuyên mục lý thuyết Phương trình, bất phương trình mũ và lôgarit của chương trình Toán 11 Chân trời sáng tạo tại tusach.vn.
Chuyên đề này đóng vai trò quan trọng trong việc xây dựng nền tảng kiến thức toán học vững chắc, phục vụ cho các bài toán nâng cao và các kỳ thi quan trọng.
Chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải quyết các bài tập.
1. Phương trình mũ cơ bản Phương trình mũ cơ bản có dạng \({a^x} = b\)(với \(a > 0,a \ne 1\)).
1. Phương trình mũ cơ bản
Phương trình mũ cơ bản có dạng \({a^x} = b\)(với \(a > 0,a \ne 1\)).
- Nếu b > 0 thì phương trình có nghiệm duy nhất \(x = {\log _a}b\).
- Nếu b \( \le \) 0 thì phương trình vô nghiệm.
Chú ý: Với \(a > 0,a \ne 1\)
a) \({a^x} = {a^\alpha } \Leftrightarrow x = \alpha \).
b) Tổng quát hơn, \({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)
Minh họa bằng đồ thị:
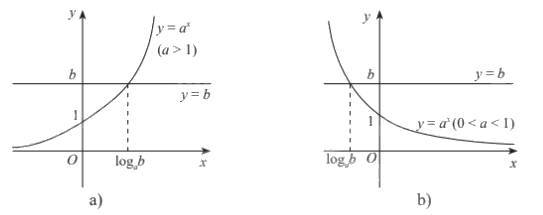
2. Phương trình lôgarit cơ bản
Phương trình lôgarit cơ bản có dạng \({\log _a}x = b\left( {a > 0,a \ne 1} \right)\).
Phương trình luôn có nghiệm duy nhất \(x = {a^b}\).
Chú ý: Với \(a > 0,a \ne 1\)
a) \({\log _a}u\left( x \right) = b \Leftrightarrow u\left( x \right) = {a^b}\).
b) \({\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.\).
Có thể thay \(u\left( x \right) > 0\) bằng \(v\left( x \right) > 0\) (chọn bất phương trình đơn giản hơn)
Minh họa bằng đồ thị:
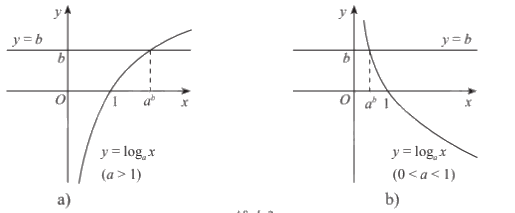
3. Bất phương trình mũ cơ bản
Bất phương trình mũ cơ bản có dạng \({a^x} > b\) (hoặc \({a^x} \ge b,{a^x} < b,{a^x} \le b\)) với \(a > 0,a \ne 1\).
Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:
Nếu a > 1 thì \({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) > v\left( x \right)\).
Nếu 0 < a < 1 thì \({a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) < v\left( x \right)\).
4. Bất phương trình lôgarit cơ bản
Bất phương trình lôgarit cơ bản có dạng \({\log _a}x > b\)(hoặc \({\log _a}x \ge b,{\log _a}x < b,{\log _a}x \le b\)) với \(a > 0,a \ne 1\).
Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:
Nếu a > 1 thì \({\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}v\left( x \right) > 0\\u\left( x \right) > v\left( x \right)\end{array} \right.\).
Nếu 0 < a < 1 thì \({\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) < v\left( x \right)\end{array} \right.\).
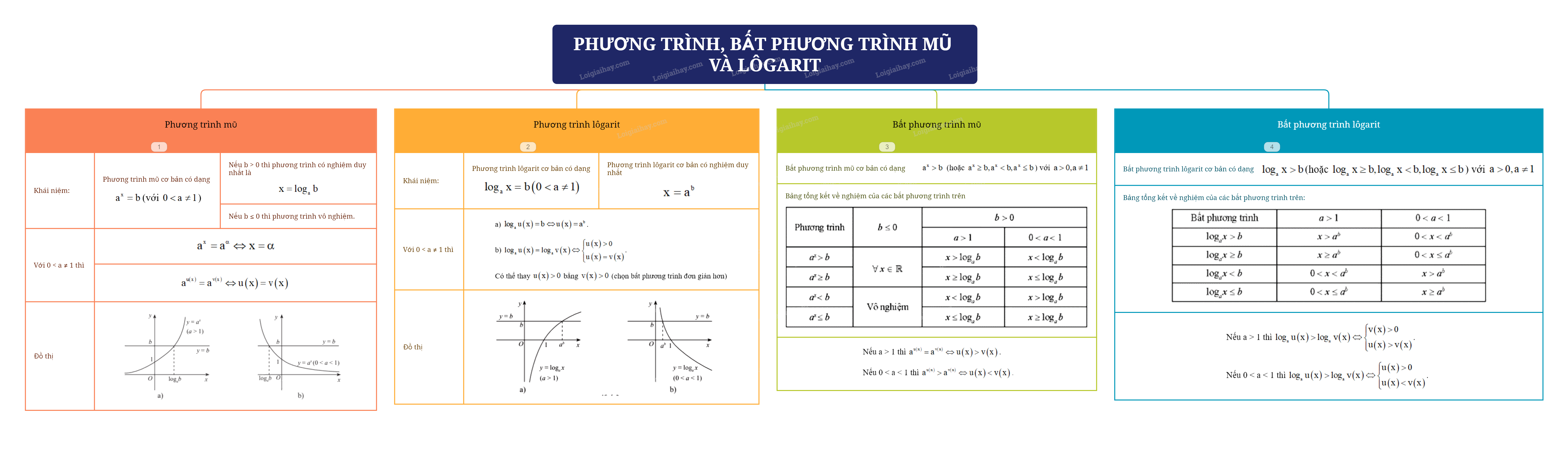
Lý Thuyết Phương Trình, Bất Phương Trình Mũ và Lôgarit - Toán 11 Chân Trời Sáng Tạo: Tổng Quan
Chuyên đề Phương trình, bất phương trình mũ và lôgarit là một phần quan trọng của chương trình Toán 11 Chân trời sáng tạo. Nó không chỉ cung cấp kiến thức nền tảng mà còn rèn luyện tư duy logic và kỹ năng giải quyết vấn đề cho học sinh. Dưới đây là tổng quan chi tiết về các nội dung chính của chuyên đề này.
1. Phương Trình Mũ
Phương trình mũ là phương trình có chứa ẩn số trong số mũ. Để giải phương trình mũ, chúng ta thường sử dụng các phương pháp sau:
- Đưa về cùng cơ số: Nếu có thể, hãy đưa cả hai vế của phương trình về cùng một cơ số.
- Lấy lôgarit hai vế: Sử dụng hàm lôgarit để loại bỏ số mũ.
- Đặt ẩn phụ: Trong một số trường hợp, việc đặt ẩn phụ có thể giúp đơn giản hóa phương trình.
Ví dụ: Giải phương trình 2x = 8. Ta có thể viết 8 = 23, suy ra x = 3.
2. Bất Phương Trình Mũ
Bất phương trình mũ tương tự như phương trình mũ, nhưng thay vì dấu bằng, chúng ta có dấu bất đẳng thức. Khi giải bất phương trình mũ, cần chú ý đến:
- Cơ số: Nếu cơ số lớn hơn 1, bất đẳng thức giữ nguyên chiều khi lấy lôgarit. Nếu cơ số nhỏ hơn 1, bất đẳng thức đổi chiều khi lấy lôgarit.
Ví dụ: Giải bất phương trình 3x > 9. Ta có thể viết 9 = 32, suy ra x > 2.
3. Phương Trình Lôgarit
Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức lôgarit. Để giải phương trình lôgarit, chúng ta thường sử dụng:
- Định nghĩa lôgarit: Sử dụng định nghĩa logab = c ⇔ ac = b để chuyển phương trình về dạng mũ.
- Đổi cơ số lôgarit: Sử dụng công thức đổi cơ số để đưa về cùng một cơ số.
Ví dụ: Giải phương trình log2(x + 1) = 3. Ta có x + 1 = 23 = 8, suy ra x = 7.
4. Bất Phương Trình Lôgarit
Bất phương trình lôgarit tương tự như phương trình lôgarit, nhưng thay vì dấu bằng, chúng ta có dấu bất đẳng thức. Khi giải bất phương trình lôgarit, cần chú ý đến:
- Điều kiện xác định: Đảm bảo rằng biểu thức trong lôgarit luôn dương.
- Cơ số: Nếu cơ số lớn hơn 1, bất đẳng thức giữ nguyên chiều khi bỏ lôgarit. Nếu cơ số nhỏ hơn 1, bất đẳng thức đổi chiều khi bỏ lôgarit.
Ví dụ: Giải bất phương trình log0.5(x - 2) > 1. Ta có x - 2 < (0.5)1 = 0.5, suy ra x < 2.5. Đồng thời, x - 2 > 0, suy ra x > 2. Vậy 2 < x < 2.5.
5. Các Dạng Bài Tập Thường Gặp
Chuyên đề này thường xuất hiện các dạng bài tập sau:
- Giải phương trình mũ cơ bản và nâng cao.
- Giải bất phương trình mũ cơ bản và nâng cao.
- Giải phương trình lôgarit cơ bản và nâng cao.
- Giải bất phương trình lôgarit cơ bản và nâng cao.
- Ứng dụng phương trình, bất phương trình mũ và lôgarit vào các bài toán thực tế.
6. Lời Khuyên Khi Học Tập
Để học tốt chuyên đề này, bạn nên:
- Nắm vững định nghĩa và các tính chất của lũy thừa và lôgarit.
- Luyện tập thường xuyên các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi và phần mềm giải toán.
- Tham khảo các tài liệu học tập và bài giảng trực tuyến.
Hy vọng với những thông tin trên, bạn sẽ có một cái nhìn tổng quan và nắm vững kiến thức về Lý thuyết Phương trình, bất phương trình mũ và lôgarit - Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!