Bài 6 trang 74 SGK Toán 11 tập 2 – Chân trời sáng tạo
Tổng quan nội dung
Bài 6 trang 74 SGK Toán 11 Tập 2 – Chân trời sáng tạo
Bài 6 trang 74 SGK Toán 11 Tập 2 thuộc chương trình học Toán 11, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các hàm số lượng giác cơ bản, tính chất của chúng và các phương pháp giải phương trình lượng giác.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m.
Đề bài
Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp.
Phương pháp giải - Xem chi tiết
Sử dụng định lí Pitago.
Lời giải chi tiết
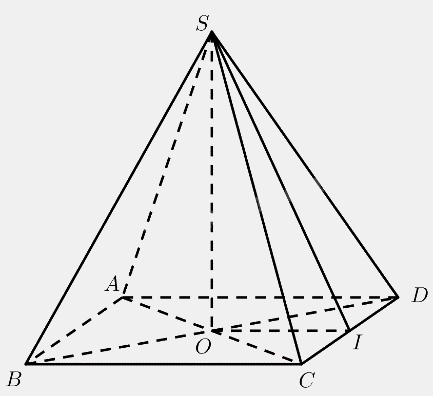
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\) có \(O\) là tâm của đáy. Kẻ \(SI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right)\).
Ta có: \(SO = 21,6;C{\rm{D}} = 34\)
\(AC = \sqrt {A{B^2} + B{C^2}} = 34\sqrt 2 \Rightarrow OC = \frac{1}{2}AC = 17\sqrt 2 \)
\(\Delta SOC\) vuông tại \(O\)\( \Rightarrow SC = \sqrt {S{O^2} + O{C^2}} \approx 32,3\)
Vậy độ dài cạnh bên bằng \(32,3\left( m \right)\)
Tam giác \(SCD\) cân tại \(S\)
\( \Rightarrow SI\) vừa là trung tuyến, vừa là đường cao của tam giác
\( \Rightarrow I\) là trung điểm của \(CD\).
Mà \(O\) là trung điểm của \(AD\)
\( \Rightarrow OI\) là đường trung bình của tam giác \(ACD\)
\( \Rightarrow OI = \frac{1}{2}BC = 17\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI\)
\( \Rightarrow \Delta SOI\) vuông tại \(O\)\( \Rightarrow SI = \sqrt {S{O^2} + O{I^2}} \approx 27,5\)
\({S_{SC{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.SI \approx 467,5\)
Diện tích xung quanh của kim tự tháp là: \({S_{xq}} = 4{S_{SC{\rm{D}}}} \approx 1870\left( {{m^2}} \right)\)
Bài 6 trang 74 SGK Toán 11 Tập 2 – Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 6 trang 74 SGK Toán 11 Tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số lượng giác và phương pháp giải phương trình lượng giác. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 6 yêu cầu giải các phương trình lượng giác sau:
- a) sin(x) = 1/2
- b) cos(x) = -√3/2
- c) tan(x) = 1
- d) cot(x) = 0
Lời giải chi tiết
a) sin(x) = 1/2
Phương trình sin(x) = 1/2 có nghiệm là:
- x = π/6 + k2π (k ∈ Z)
- x = 5π/6 + k2π (k ∈ Z)
b) cos(x) = -√3/2
Phương trình cos(x) = -√3/2 có nghiệm là:
- x = 5π/6 + k2π (k ∈ Z)
- x = 7π/6 + k2π (k ∈ Z)
c) tan(x) = 1
Phương trình tan(x) = 1 có nghiệm là:
- x = π/4 + kπ (k ∈ Z)
d) cot(x) = 0
Phương trình cot(x) = 0 có nghiệm là:
- x = π/2 + kπ (k ∈ Z)
Hướng dẫn giải bài tập tương tự
Để giải các phương trình lượng giác tương tự, bạn cần:
- Xác định giá trị lượng giác đặc biệt của các góc cơ bản (0, π/6, π/4, π/3, π/2, π, 3π/2, 2π).
- Sử dụng các công thức lượng giác để biến đổi phương trình về dạng cơ bản.
- Tìm nghiệm của phương trình lượng giác cơ bản.
- Viết nghiệm tổng quát của phương trình.
Ví dụ minh họa
Giải phương trình sin(2x) = √2/2
Ta có:
- 2x = π/4 + k2π (k ∈ Z) => x = π/8 + kπ (k ∈ Z)
- 2x = 3π/4 + k2π (k ∈ Z) => x = 3π/8 + kπ (k ∈ Z)
Lưu ý quan trọng
Khi giải phương trình lượng giác, cần kiểm tra lại nghiệm để đảm bảo chúng không phải là nghiệm ngoại lai. Ngoài ra, cần chú ý đến điều kiện xác định của phương trình.
Tổng kết
Bài 6 trang 74 SGK Toán 11 Tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình lượng giác. Việc nắm vững kiến thức về các hàm số lượng giác và các công thức lượng giác là điều cần thiết để giải bài tập này một cách hiệu quả.
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh sẽ hiểu rõ hơn về bài tập này và đạt kết quả tốt trong môn Toán 11.