Bài 3 trang 120 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 3 trang 120 SGK Toán 11 tập 1 - Chân trời sáng tạo
Bài 3 thuộc chương trình học Toán 11 tập 1, sách Chân trời sáng tạo, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến giới hạn của hàm số. Bài tập này giúp học sinh hiểu sâu hơn về khái niệm giới hạn và ứng dụng của nó trong việc tính toán.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
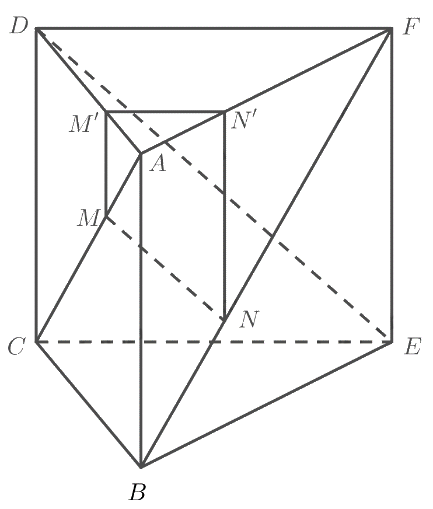
Cho hai hình vuông \(ABCD\) và \(ABEF\) ở trong hai mặt phẳng khác nhau. Trên các đường chéo \(AC\) và \(BF\) lần lượt lấy các điểm \(M,N\) sao cho \(AM = BN\). Các đường thẳng song song với \(AB\) vẽ từ \(M,N\) lần lượt cắt \(AD,AF\) tại \(M',N'\).
Đề bài
Cho hai hình vuông \(ABCD\) và \(ABEF\) ở trong hai mặt phẳng khác nhau. Trên các đường chéo \(AC\) và \(BF\) lần lượt lấy các điểm \(M,N\) sao cho \(AM = BN\). Các đường thẳng song song với \(AB\) vẽ từ \(M,N\) lần lượt cắt \(AD,AF\) tại \(M',N'\).
a) Chứng minh \(\left( {CBE} \right)\parallel \left( {ADF} \right)\).
b) Chứng minh \(\left( {DEF} \right)\parallel \left( {MNN'M'} \right)\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng định lí Thalès trong tam giác.
‒ Sử dụng định lí 1: Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng \(\left( Q \right)\) thì \(\left( P \right)\) song song với \(\left( Q \right)\).
Lời giải chi tiết
a) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AD\parallel BC\)
Mà \(A{\rm{D}} \subset \left( {ADF} \right)\)
\( \Rightarrow BC\parallel \left( {A{\rm{D}}F} \right)\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AF\parallel BE\)
Mà \(A{\rm{F}} \subset \left( {ADF} \right)\)
\( \Rightarrow BE\parallel \left( {A{\rm{D}}F} \right)\)
Ta có:
\(\left. \begin{array}{l}BC\parallel \left( {A{\rm{D}}F} \right)\\BE\parallel \left( {A{\rm{D}}F} \right)\\BC,BE \subset \left( {CBE} \right)\end{array} \right\} \Rightarrow \left( {CBE} \right)\parallel \left( {A{\rm{D}}F} \right)\)
b) Do \(ABCD\) và \(ABEF\) là hai hình vuông có chung cạnh \(AB\) nên các đường chéo \(AC,BF\) bằng nhau.
Theo đề bài ta có: \(AM = BN\)
\( \Rightarrow \)\(\frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\)
Ta có:
\(MM'\parallel C{\rm{D}} \Rightarrow \frac{{AM}}{{AC}} = \frac{{AM'}}{{A{\rm{D}}}}\)
\(NN'\parallel AB \Rightarrow \frac{{BN}}{{BF}} = \frac{{AN'}}{{AF}}\)
\(\left. \begin{array}{l} \Rightarrow \frac{{AM'}}{{A{\rm{D}}}} = \frac{{AN'}}{{AF}} \Rightarrow M'N'\parallel DF\\M'N' \subset \left( {MNN'M'} \right)\end{array} \right\} \Rightarrow DF\parallel \left( {MNN'M'} \right)\)
\(\left. \begin{array}{l}NN'\parallel EF\\{\rm{NN}}' \subset \left( {MNN'M'} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {MNN'M'} \right)\)
\(\left. \begin{array}{l}DF\parallel \left( {MNN'M'} \right)\\EF\parallel \left( {MNN'M'} \right)\\C{\rm{D}},DF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow \left( {DEF} \right)\parallel \left( {MNN'M'} \right)\)
Bài 3 trang 120 SGK Toán 11 tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 3 trang 120 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về giới hạn của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 3 yêu cầu học sinh tính giới hạn của các hàm số tại một điểm cho trước. Các hàm số có thể có dạng đơn giản hoặc phức tạp hơn, đòi hỏi học sinh phải áp dụng các quy tắc và định lý về giới hạn để giải quyết.
Lời giải chi tiết
Để giải bài 3, chúng ta cần thực hiện các bước sau:
- Xác định dạng của hàm số: Xem hàm số có dạng đơn giản hay phức tạp.
- Áp dụng các quy tắc về giới hạn: Sử dụng các quy tắc như giới hạn của tổng, hiệu, tích, thương, và giới hạn của hàm hợp.
- Sử dụng các định lý về giới hạn: Áp dụng các định lý như giới hạn của hàm số khi x tiến tới vô cùng.
- Kiểm tra kết quả: Đảm bảo kết quả tính toán là chính xác và hợp lý.
Ví dụ: Giả sử bài tập yêu cầu tính lim (x→2) (x2 - 4) / (x - 2). Chúng ta có thể giải như sau:
- Phân tích tử số: x2 - 4 = (x - 2)(x + 2)
- Rút gọn biểu thức: (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2
- Tính giới hạn: lim (x→2) (x + 2) = 2 + 2 = 4
Các dạng bài tập thường gặp
Trong bài 3, học sinh có thể gặp các dạng bài tập sau:
- Tính giới hạn của hàm số đa thức.
- Tính giới hạn của hàm số hữu tỉ.
- Tính giới hạn của hàm số chứa căn thức.
- Tính giới hạn của hàm số lượng giác.
Mẹo giải bài tập
Để giải bài tập về giới hạn một cách hiệu quả, học sinh nên:
- Nắm vững các quy tắc và định lý về giới hạn.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
- Tham khảo các tài liệu tham khảo và lời giải trên mạng.
Ứng dụng của giới hạn
Giới hạn là một khái niệm quan trọng trong toán học, có nhiều ứng dụng trong các lĩnh vực khác nhau, như:
- Tính đạo hàm và tích phân.
- Nghiên cứu sự biến thiên của hàm số.
- Giải các bài toán vật lý và kỹ thuật.
Kết luận
Bài 3 trang 120 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Bằng cách nắm vững các quy tắc, định lý và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và ứng dụng kiến thức này vào các lĩnh vực khác.
tusach.vn hy vọng rằng lời giải chi tiết và hướng dẫn này sẽ giúp các em học sinh hiểu rõ hơn về bài tập và đạt kết quả tốt trong học tập.