Giải mục 4 trang 75, 76 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 4 trang 75, 76 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 75, 76 SGK Toán 11 tập 1 - Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng và kiến thức đã học.
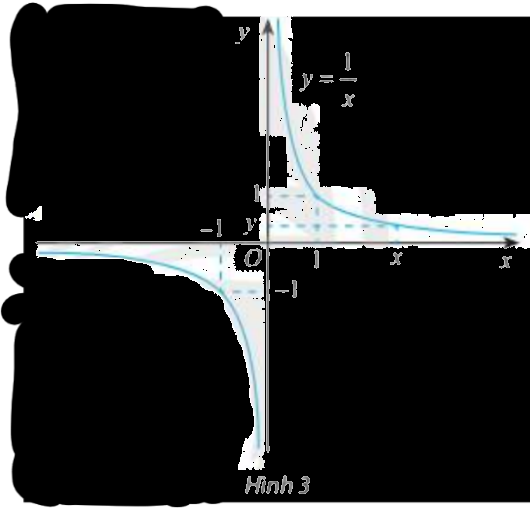
Cho hàm số \(f\left( x \right) = \frac{1}{x}\) có đồ thị như Hình 3.
Hoạt động 4
Cho hàm số \(f\left( x \right) = \frac{1}{x}\) có đồ thị như Hình 3.
a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng lớn (dần tới \( + \infty \))?
b) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng bé (dần tới \( - \infty \))?
Phương pháp giải:
Để điền giá trị vào bảng, ta thay giá trị của \(x\) vào hàm số \(f\left( x \right) = \frac{1}{x}\).
Lời giải chi tiết:
a)
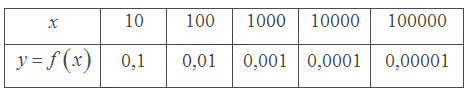
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).
Thực hành 4
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}}\).
Phương pháp giải:
Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}\left( {\frac{1}{{{x^2}}} - 3} \right)}}{{{x^2}\left( {1 + \frac{{2x}}{{{x^2}}}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{{{x^2}}} - 3}}{{1 + \frac{2}{x}}} = \frac{{\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{x^2}}} - \mathop {\lim }\limits_{x \to + \infty } 3}}{{\mathop {\lim }\limits_{x \to + \infty } 1 + \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x}}} = \frac{{0 - 3}}{{1 + 0}} = - 3\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{1 + \frac{1}{x}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\frac{{\mathop {\lim }\limits_{x \to - \infty } 2}}{{\mathop {\lim }\limits_{x \to - \infty } 1 + \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}}} = 0.\frac{2}{{1 + 0}} = 0\).
Vận dụng 1
Một cái hồ đang chứa \(200{m^3}\) nước mặn với nồng độ muối \(10kg/{m^3}\). Người ta ngọt hóa nước trong hồ bằng cách bơm nước ngọt vào hồ với tốc độ \(2{m^3}/\)phút.
a) Viết biểu thức \(C\left( t \right)\) biểu thị nồng độ muối trong hồ sau \(t\) phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right)\) và giải thích ý nghĩa.
Phương pháp giải:
a) Dựa vào dữ kiện của đề bài, biểu thị mối liên hệ giữa các đại lượng khối lượng muối, lượng nước trong hồ và nồng độ muối để viết biểu thức \(C\left( t \right)\).
b) Vận dụng phương pháp tính giới hạn của hàm số tại vô cực:
Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.
Lời giải chi tiết:
a) Khối lượng muối có trong hồ là: \(200.10 = 2000\left( {kg} \right)\).
Sau \(t\) phút kể từ khi bắt đầu bơm, lượng nước trong hồ là: \(200 + 2t\left( {{m^3}} \right)\).
Nồng độ muối tại thời điểm \(t\) phút kể từ khi bắt đầu bơm là: \(C\left( t \right) = \frac{{2000}}{{200 + 2t}}\left( {kg/{m^3}} \right)\)
b) \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{200 + 2t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{t\left( {\frac{{200}}{t} + 2} \right)}} = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{\frac{{200}}{t} + 2}}\)
\( = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\frac{{\mathop {\lim }\limits_{t \to + \infty } 2000}}{{\mathop {\lim }\limits_{t \to + \infty } \frac{{200}}{t} + \mathop {\lim }\limits_{t \to + \infty } 2}} = 0.\frac{{2000}}{{0 + 2}} = 0\)
Ý nghĩa: Khi \(t\) càng lớn thì nồng độ muối càng dần về 0, tức là đến một lúc nào đó nồng độ muối trong hồ không đáng kể, nước trong hồ gần như là nước ngọt.
Giải mục 4 trang 75, 76 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 4 trang 75, 76 SGK Toán 11 tập 1 - Chân trời sáng tạo là một phần quan trọng trong chương trình học, tập trung vào việc vận dụng các kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Để giúp các em học sinh hiểu rõ hơn và tự tin làm bài, tusach.vn xin giới thiệu lời giải chi tiết và hướng dẫn giải các bài tập trong mục này.
Nội dung chính của Mục 4
Mục 4 thường bao gồm các dạng bài tập sau:
- Xác định tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Xác định tính đơn điệu của hàm số.
- Vẽ đồ thị hàm số.
- Giải các bài toán liên quan đến ứng dụng của hàm số.
Hướng dẫn giải chi tiết các bài tập
Để giải các bài tập trong mục này, các em cần nắm vững các kiến thức sau:
- Định nghĩa hàm số và các yếu tố của hàm số (tập xác định, tập giá trị, tính đơn điệu).
- Các phương pháp vẽ đồ thị hàm số (sử dụng bảng giá trị, sử dụng đạo hàm).
- Các ứng dụng của hàm số trong thực tế.
Bài 1: (Trang 75)
Đề bài: Xác định tập xác định của hàm số y = √(2x - 1).
Lời giải: Hàm số y = √(2x - 1) xác định khi và chỉ khi 2x - 1 ≥ 0. Giải bất phương trình này, ta được x ≥ 1/2. Vậy tập xác định của hàm số là D = [1/2, +∞).
Bài 2: (Trang 76)
Đề bài: Tìm tập giá trị của hàm số y = x2 - 4x + 3.
Lời giải: Hàm số y = x2 - 4x + 3 là một hàm bậc hai có hệ số a = 1 > 0. Do đó, hàm số có giá trị nhỏ nhất tại đỉnh của parabol. Hoành độ đỉnh là x = -b/(2a) = 4/(2*1) = 2. Giá trị nhỏ nhất của hàm số là y = 22 - 4*2 + 3 = -1. Vậy tập giá trị của hàm số là [ -1, +∞).
Mẹo giải nhanh
Để giải nhanh các bài tập về hàm số, các em có thể sử dụng các mẹo sau:
- Sử dụng các công thức đạo hàm để xác định tính đơn điệu của hàm số.
- Sử dụng các tính chất đối xứng của đồ thị hàm số để vẽ đồ thị nhanh hơn.
- Luyện tập thường xuyên để nắm vững các kiến thức và kỹ năng.
Tài liệu tham khảo thêm
Ngoài SGK Toán 11 tập 1 - Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11.
- Các trang web học Toán trực tuyến.
- Các video hướng dẫn giải Toán trên YouTube.
Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn giải các bài tập trong mục 4 trang 75, 76 SGK Toán 11 tập 1 - Chân trời sáng tạo, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán. Chúc các em thành công!
| Bài tập | Lời giải |
|---|---|
| Bài 1 (Trang 75) | x ≥ 1/2 |
| Bài 2 (Trang 76) | y ≥ -1 |
| Nguồn: tusach.vn | |