Đề bài
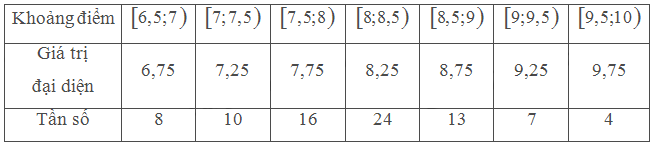
Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:
Hãy ước lượng số trung bình, tứ phân vị và mốt của mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính số trung bình, mốt, tứ phân vị của mẫu số liệu ghép nhóm.
Lời giải chi tiết
Ta có:
Tổng số học sinh: \(n = 8 + 10 + 16 + 24 + 13 + 7 + 4 = 82\)
• Điểm trung bình môn Toán của các học sinh lớp 11 trên là:
\(\bar x = \frac{{8.6,75 + 10.7,25 + 16.7,75 + 24.8,25 + 13.8,75 + 7.9,25 + 4.9,75}}{{82}} = 8,12\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {8;8,5} \right)\).
Do đó: \({u_m} = 8;{n_{m - 1}} = 16;{n_m} = 24;{n_{m + 1}} = 13;{u_{m + 1}} - {u_m} = 8,5 - 8 = 0,5\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{24 - 16}}{{\left( {24 - 16} \right) + \left( {24 - 13} \right)}}.0,5 \approx 8,21\)
• Gọi \({x_1};{x_2};...;{x_{82}}\) là điểm của các học sinh lớp 11 được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_8} \in \begin{array}{*{20}{c}}{\left[ {6,5;7} \right)}\end{array};{x_9},...,{x_{18}} \in \begin{array}{*{20}{c}}{\left[ {7;7,5} \right)}\end{array};{x_{19}},...,{x_{34}} \in \begin{array}{*{20}{c}}{\left[ {7,5;8} \right)}\end{array};{x_{35}},...,{x_{58}} \in \begin{array}{*{20}{c}}{\left[ {8;8,5} \right)}\end{array};\\{x_{59}},...,{x_{71}} \in \begin{array}{*{20}{c}}{\left[ {8,5;9} \right)}\end{array};{x_{72}},...,{x_{78}} \in \begin{array}{*{20}{c}}{\left[ {9;9,5} \right)}\end{array};{x_{79}},...,{x_{82}} \in \begin{array}{*{20}{c}}{\left[ {9,5;10} \right)}\end{array}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{41}} + {x_{42}}} \right)\)
Ta có: \(n = 82;{n_m} = 24;C = 8 + 10 + 16 = 34;{u_m} = 8;{u_{m + 1}} = 8,5\)
Do \({x_{41}},{x_{42}} \in \begin{array}{*{20}{l}}{\left[ {8;8,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{\frac{{82}}{2} - 34}}{{24}}.\left( {8,5 - 8} \right) \approx 8,15\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_{21}}\).
Ta có: \(n = 82;{n_m} = 16;C = 8 + 10 = 18;{u_m} = 7,5;{u_{m + 1}} = 8\)
Do \({x_{21}} \in \begin{array}{*{20}{l}}{\left[ {7,5;8} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 7,5 + \frac{{\frac{{82}}{4} - 18}}{{16}}.\left( {8 - 7,5} \right) \approx 7,58\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{62}}\).
Ta có: \(n = 82;{n_j} = 13;C = 8 + 10 + 16 + 24 = 58;{u_j} = 8,5;{u_{j + 1}} = 9\)
Do \({x_{62}} \in \begin{array}{*{20}{l}}{\left[ {8,5;9} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 8,5 + \frac{{\frac{{3.82}}{4} - 58}}{{13}}.\left( {9 - 8,5} \right) \approx 8,63\)
