Bài 9 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 9 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài 9 trang 24 SGK Toán 11 Tập 1 thuộc chương trình học Toán 11, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về các loại hàm số, tính đơn điệu, cực trị và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là (frac{{2pi }}{3})và số đo góc (OA, OM) là (alpha ).
Đề bài
Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là \(\frac{{2\pi }}{3}\) và số đo góc (OA, OM) là \(\alpha \).
a) Tính sin\(\alpha \) và cos \(\alpha \).
b) Tính sin của các góc lượng giác (OA, ON) và (OA, OP) từ đó tính chiều cao của các điểm N và P so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.

Phương pháp giải - Xem chi tiết
Dựa vào hình vẽ để tìm sin\(\alpha \)và cos \(\alpha \); sử dụng công thức cộng để tính sin của các góc lượng giác (OA, ON) và (OA, OP).
Lời giải chi tiết
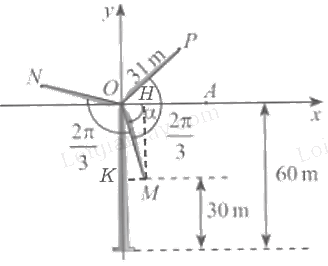
a, Từ điểm M kẻ MH vuông góc với Ox, MK vuông góc với Oy.
Ta có: MH = 60 – 30 = 30 m.
Khi đó hoành độ điểm M là 30.
⇒ \(\;\sin \alpha {\rm{ }} = \;\frac{{MH}}{{OM}} = \;\frac{{30}}{{31}}\)
\( \Rightarrow \cos \alpha = \sqrt {1 - {{\left( {\frac{{30}}{{31}}} \right)}^2}} = \frac{{\sqrt {61} }}{{31}}\)
b, Vì các cánh quạt tạo thành 3 góc bằng nhau nên \(\widehat {MOP} = \widehat {NOP} = \widehat {MON} = {120^0}\)
\( \Rightarrow \widehat {AOP} = \widehat {MOP} - \widehat {MOA}\)
\( \Leftrightarrow \sin \widehat {AOP} = \sin \left( {\widehat {MOP} - \widehat {MOA}} \right) = \sin \widehat {MOP}.\cos \widehat {MOA} - \cos \widehat {MOP}.\sin \widehat {MOA}\)
\( = \sin \frac{{2\pi }}{3}.\cos \alpha - \cos \frac{{2\pi }}{3}.\sin \alpha \approx 0,7\)
Vì vậy chiều cao của điểm P so với mặt đất là:
31. \(\sin \widehat {AOP}\) + 60 = 31.0,7+ 60 \( \approx \) 81,76 m.
Ta có:
\(\cos \widehat {AOP} \approx \sqrt {1 - 0,{7^2}} = 0,71\)
\(\widehat {AON} = \widehat {AOP} + \widehat {PON}\)
\(\begin{array}{l} \Leftrightarrow \sin \widehat {AON} = \sin \left( {\widehat {AOP} + \widehat {PON}} \right)\\ \Leftrightarrow \sin \widehat {AON} = \sin \widehat {AOP}.\cos \widehat {PON} + \cos \widehat {AOP}.\sin \widehat {PON}\\ \Leftrightarrow \sin \widehat {AON} = 0,7.\cos \frac{{2\pi }}{3} + 0,71.\sin \frac{{2\pi }}{3} \approx 0,26\end{array}\)
\( \Rightarrow \sin \left( {OA,ON} \right) = \sin \widehat {AON} \approx 0,26\)
Vì vậy chiều cao của điểm N so với mặt đất là:
31. \(\sin \widehat {AON}\) + 60 = 31.0,26+ 60\( \approx \) 68,2 m.
Bài 9 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 9 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số và ứng dụng của đạo hàm. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 9 yêu cầu học sinh giải các bài toán liên quan đến việc xác định tính đơn điệu của hàm số, tìm cực trị và vẽ đồ thị hàm số. Cụ thể, bài tập có thể bao gồm:
- Xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm điểm cực đại, cực tiểu của hàm số.
- Vẽ đồ thị hàm số dựa trên các thông tin đã tìm được.
Lời giải chi tiết
Để giải bài 9 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo, học sinh cần thực hiện các bước sau:
- Bước 1: Tính đạo hàm của hàm số.
- Bước 2: Tìm các điểm dừng của hàm số (điểm mà đạo hàm bằng 0 hoặc không xác định).
- Bước 3: Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến của hàm số.
- Bước 4: Xác định các điểm cực đại, cực tiểu của hàm số.
- Bước 5: Vẽ đồ thị hàm số.
Ví dụ: Xét hàm số y = x3 - 3x2 + 2.
Bước 1: Đạo hàm của hàm số là y' = 3x2 - 6x.
Bước 2: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
Bước 3: Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Bước 4: Hàm số đạt cực đại tại x = 0, ymax = 2 và đạt cực tiểu tại x = 2, ymin = -2.
Bước 5: Vẽ đồ thị hàm số dựa trên các thông tin đã tìm được.
Mẹo giải nhanh
Để giải nhanh bài 9 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo, học sinh có thể sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị. Ngoài ra, việc nắm vững các công thức và định lý liên quan đến hàm số và đạo hàm cũng rất quan trọng.
Bài tập tương tự
Để rèn luyện kỹ năng giải toán, học sinh có thể làm thêm các bài tập tương tự trong SGK và sách bài tập Toán 11 Tập 1 - Chân trời sáng tạo. Một số bài tập tham khảo:
- Bài 10 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo
- Bài 11 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Kết luận
Bài 9 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và ứng dụng của đạo hàm. Bằng cách thực hiện các bước giải chi tiết và rèn luyện kỹ năng giải toán thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự.
Chúc các em học tốt!