Bài 2 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo
Tổng quan nội dung
Bài 2 trang 56 SGK Toán 11 Tập 2 – Chân trời sáng tạo
Bài 2 trang 56 SGK Toán 11 Tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài tập về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tính đạo hàm của hàm số và giải các bài toán liên quan.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tứ diện đều (ABCD). Chứng minh rằng (AB bot CD).
Đề bài
Cho tứ diện đều \(ABCD\). Chứng minh rằng \(AB \bot CD\).
Phương pháp giải - Xem chi tiết
Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).
Lời giải chi tiết
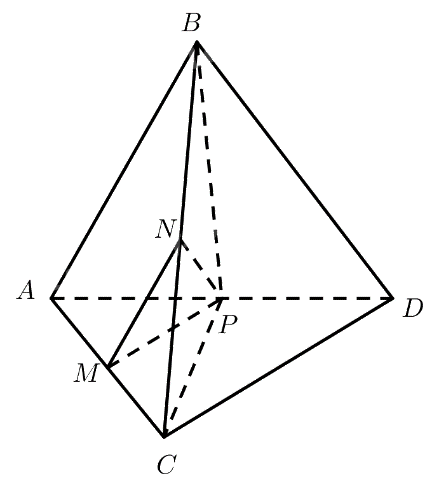
Giả sử tứ diện đều \(ABCD\) có cạnh bằng \(a\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AC,BC,A{\rm{D}}\).
\(M\) là trung điểm của \(AC\)
\(N\) là trung điểm của \(BC\)
\( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow MN\parallel AB,MN = \frac{1}{2}AB = \frac{a}{2}\)
\(M\) là trung điểm của \(AC\)
\(P\) là trung điểm của \(AD\)
\( \Rightarrow MP\) là đường trung bình của tam giác \(AC{\rm{D}}\)
\( \Rightarrow MP\parallel C{\rm{D,MP}} = \frac{1}{2}C{\rm{D}} = \frac{a}{2}\)
Ta có: \(MN\parallel AB,MP\parallel C{\rm{D}} \Rightarrow \left( {AB,C{\rm{D}}} \right) = \left( {MN,MP} \right) = \widehat {NMP}\)
Ta có: \(BP\) là trung tuyến của tam giác \(ABD\)\( \Rightarrow BP = \frac{{\sqrt {2\left( {A{B^2} + B{{\rm{D}}^2}} \right) - A{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(CP\) là trung tuyến của tam giác \(ACD\)\( \Rightarrow CP = \frac{{\sqrt {2\left( {A{C^2} + C{{\rm{D}}^2}} \right) - A{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(NP\) là trung tuyến của tam giác \(BCP\)\( \Rightarrow NP = \frac{{\sqrt {2\left( {B{P^2} + C{{\rm{P}}^2}} \right) - B{C^2}} }}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác \(MNP\) có:
\(\cos \widehat {NMP} = \frac{{M{N^2} + M{P^2} - N{P^2}}}{{2.MN.MP}} = 0 \Rightarrow \widehat {NMP} = {90^ \circ }\)
Vậy \(\left( {AB,C{\rm{D}}} \right) = {90^ \circ }\).
Bài 2 trang 56 SGK Toán 11 Tập 2 – Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 2 trang 56 SGK Toán 11 Tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học về đạo hàm. Để giải bài tập này, học sinh cần nắm vững các công thức và quy tắc tính đạo hàm của các hàm số cơ bản, cũng như các quy tắc tính đạo hàm của hàm hợp và hàm ẩn.
Nội dung bài tập:
Bài tập yêu cầu tính đạo hàm của các hàm số sau:
- f(x) = x3 - 3x2 + 2x - 5
- g(x) = (2x + 1)(x2 - x + 3)
- h(x) = sin(2x + 1)
Lời giải chi tiết:
a) f(x) = x3 - 3x2 + 2x - 5
Áp dụng quy tắc đạo hàm của tổng và hiệu, ta có:
f'(x) = 3x2 - 6x + 2
b) g(x) = (2x + 1)(x2 - x + 3)
Áp dụng quy tắc đạo hàm của tích, ta có:
g'(x) = 2(x2 - x + 3) + (2x + 1)(2x - 1)
g'(x) = 2x2 - 2x + 6 + 4x2 - 2x + 2x - 1
g'(x) = 6x2 - 2x + 5
c) h(x) = sin(2x + 1)
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
h'(x) = cos(2x + 1) * 2
h'(x) = 2cos(2x + 1)
Lưu ý quan trọng:
Khi giải bài tập về đạo hàm, cần chú ý các quy tắc đạo hàm cơ bản và quy tắc đạo hàm của hàm hợp. Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự:
Để rèn luyện thêm kỹ năng giải bài tập về đạo hàm, học sinh có thể tham khảo các bài tập tương tự sau:
- Tính đạo hàm của hàm số y = x4 - 5x2 + 7x - 10
- Tính đạo hàm của hàm số y = (x + 2)(x2 - 3x + 1)
- Tính đạo hàm của hàm số y = cos(3x - 2)
Tài liệu tham khảo:
Học sinh có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về đạo hàm:
- Sách giáo khoa Toán 11 Tập 2 – Chân trời sáng tạo
- Sách bài tập Toán 11 Tập 2 – Chân trời sáng tạo
- Các trang web học toán trực tuyến uy tín
Kết luận: Bài 2 trang 56 SGK Toán 11 Tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Bằng cách nắm vững các quy tắc và công thức đạo hàm, học sinh có thể tự tin giải các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Hàm số | Đạo hàm |
|---|---|
| f(x) = x3 - 3x2 + 2x - 5 | f'(x) = 3x2 - 6x + 2 |
| g(x) = (2x + 1)(x2 - x + 3) | g'(x) = 6x2 - 2x + 5 |
| h(x) = sin(2x + 1) | h'(x) = 2cos(2x + 1) |