Giải mục 5 trang 77, 78 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 5 trang 77, 78 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết mục 5 trang 77, 78 sách giáo khoa Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những giải pháp học tập hiệu quả và dễ hiểu nhất cho các em học sinh.
Bài viết này sẽ giúp bạn hiểu rõ cách giải các bài tập trong mục này, từ đó củng cố kiến thức và tự tin hơn trong quá trình học tập.
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\) có đồ thị như Hình 4.
Hoạt động 5
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\) có đồ thị như Hình 4.
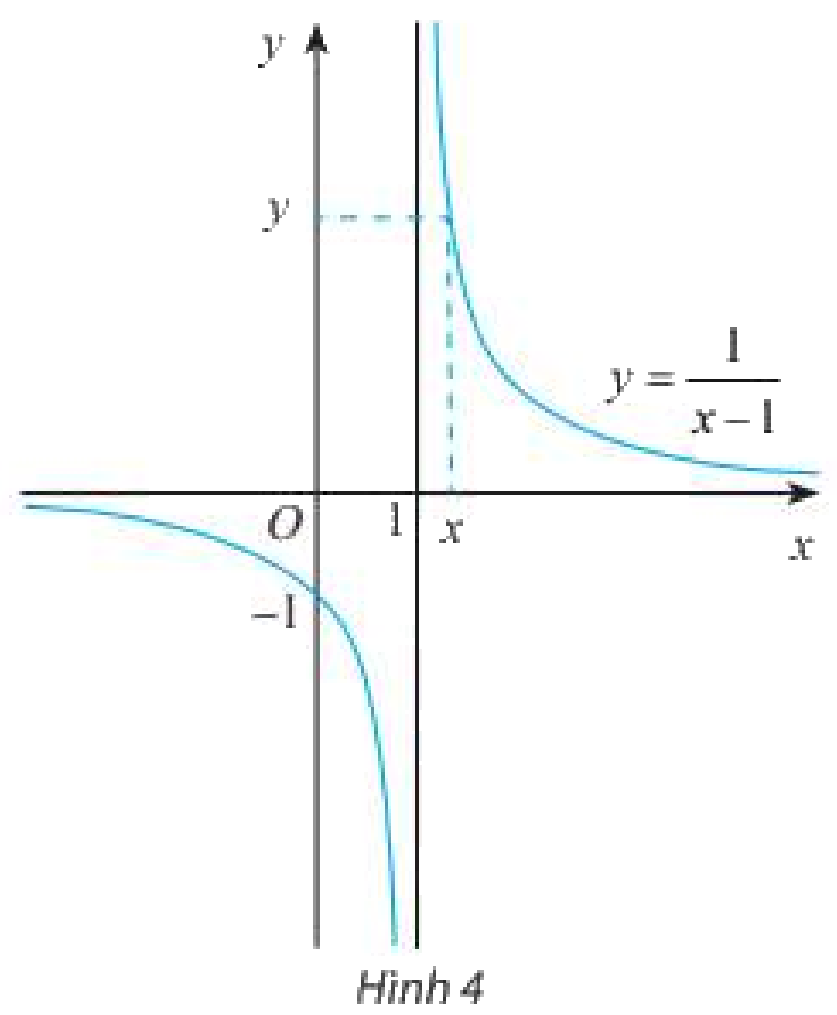
a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên phải?
b) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên trái?
Phương pháp giải:
Để điền giá trị vào bảng, ta thay giá trị của \(x\) vào hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\).
Lời giải chi tiết:
a)
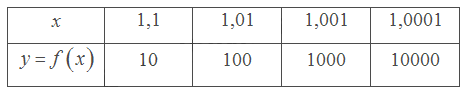
Giá trị \(f\left( x \right)\) trở nên rất lớn khi \(x\) dần tới 1 phía bên phải.
b)

Giá trị \(f\left( x \right)\) trở nên rất bé khi \(x\) dần tới 1 phía bên trái.
Thực hành 5
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}}\);
b) \(\mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right)\).
Phương pháp giải:
Bước 1: Đưa hàm số \(f\left( x \right)\) về tích của hai hàm số, trong đó một hàm số có giới hạn hữu hạn, còn một hàm số có giới hạn vô cực.
Bước 2: Áp dụng quy tắc xét dấu để tính giới hạn của tích.
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \left( {2x} \right).\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}}\)
Ta có: \(\mathop {\lim }\limits_{x \to {3^ - }} \left( {2x} \right) = 2\mathop {\lim }\limits_{x \to {3^ - }} x = 2.3 = 6;\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}} = - \infty \)
\( \Rightarrow \mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}} = - \infty \)
b) \(\mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right) = \mathop {\lim }\limits_{x \to + \infty } x\left( {3 - \frac{1}{x}} \right) = \mathop {\lim }\limits_{x \to + \infty } x.\mathop {\lim }\limits_{x \to + \infty } \left( {3 - \frac{1}{x}} \right)\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } x = + \infty ;\mathop {\lim }\limits_{x \to + \infty } \left( {3 - \frac{1}{x}} \right) = \mathop {\lim }\limits_{x \to + \infty } 3 - \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 3 - 0 = 3\)
\( \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right) = + \infty \)
Vận dụng 2
Xét tình huống ở đầu bài học. Gọi \(x\) là hoành độ điểm \(H\). Tính diện tích \(S\left( x \right)\) của hình chữ nhật \(OHMK\) theo \(x\). Diện tích này thay đổi như thế nào khi \(x \to {0^ + }\) và khi \(x \to + \infty \).
Phương pháp giải:
− Để tính diện tích \(S\left( x \right)\), ta tìm độ dài \(OH\) và \(OK\) rồi áp dụng công thức tính diện tích hình chữ nhật.
− Để xác định xem diện tích \(S\left( x \right)\) thay đổi như thế nào khi \(x \to {0^ + }\) và khi \(x \to + \infty \), ta tính giới hạn \(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right)\) và \(\mathop {\lim }\limits_{x \to + \infty } S\left( x \right)\).
Lời giải chi tiết:
Giả sử điểm \(M\) có hoành độ là \(x\).
Độ dài \(OH\) là hoành độ của điểm \(M\). Vậy \(OH = x\).
Độ dài \(OK\) là tung độ của điểm \(M\). Vậy \(OK = \frac{1}{{{x^2}}}\).
\(S\left( x \right) = OH.OK = x.\frac{1}{{{x^2}}} = \frac{1}{x}\).
\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = + \infty \). Vậy diện tích \(S\left( x \right)\) trở nên rất lớn khi \(x \to {0^ + }\).
\(\mathop {\lim }\limits_{x \to + \infty } S\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\). Vậy diện tích \(S\left( x \right)\) dần về 0 khi \(x \to + \infty \).
Giải mục 5 trang 77, 78 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 5 trang 77, 78 SGK Toán 11 tập 1 Chân trời sáng tạo tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Đây là một chương quan trọng, đặt nền móng cho các kiến thức toán học nâng cao hơn trong các lớp học tiếp theo. Việc nắm vững các khái niệm và kỹ năng trong chương này là vô cùng cần thiết.
Nội dung chính của Mục 5
Mục 5 bao gồm các bài tập tổng hợp, giúp học sinh ôn lại các kiến thức đã học về:
- Định nghĩa hàm số
- Tập xác định và tập giá trị của hàm số
- Các loại hàm số (hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit)
- Đồ thị hàm số
- Tính đơn điệu của hàm số
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 5 trang 77, 78 SGK Toán 11 tập 1 Chân trời sáng tạo:
Bài 1:
(Đề bài cụ thể của bài 1)
Lời giải:
(Giải thích chi tiết từng bước giải bài 1, kèm theo các công thức và lưu ý quan trọng)
Bài 2:
(Đề bài cụ thể của bài 2)
Lời giải:
(Giải thích chi tiết từng bước giải bài 2, kèm theo các công thức và lưu ý quan trọng)
Bài 3:
(Đề bài cụ thể của bài 3)
Lời giải:
(Giải thích chi tiết từng bước giải bài 3, kèm theo các công thức và lưu ý quan trọng)
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong mục 5 một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
- Nắm vững định nghĩa và tính chất của các loại hàm số.
- Sử dụng các công thức và quy tắc đã học một cách linh hoạt.
- Vẽ đồ thị hàm số để hình dung rõ hơn về tính chất của hàm số.
- Kiểm tra lại kết quả sau khi giải xong.
Ví dụ minh họa nâng cao
Để hiểu sâu hơn về các kiến thức trong mục 5, chúng ta cùng xem xét một ví dụ minh họa nâng cao:
(Đề bài ví dụ nâng cao)
Lời giải:
(Giải thích chi tiết lời giải ví dụ nâng cao, áp dụng các kiến thức đã học)
Luyện tập thêm
Để củng cố kiến thức và rèn luyện kỹ năng, bạn có thể tự giải thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học tập trực tuyến.
Kết luận
Hy vọng rằng, với hướng dẫn chi tiết và các mẹo giải nhanh trên, bạn đã có thể tự tin giải các bài tập trong mục 5 trang 77, 78 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc bạn học tập tốt!
| Bài tập | Mức độ khó | Lời giải |
|---|---|---|
| Bài 1 | Dễ | Xem lời giải |
| Bài 2 | Trung bình | Xem lời giải |
| Bài 3 | Khó | Xem lời giải |