Giải mục 3 trang 28, 29, 30, 31, 32 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 28, 29, 30, 31, 32 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác nhất cho các bài tập trong sách giáo khoa Toán 11 tập 1 Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng hỗ trợ bạn một cách tốt nhất.
Mục 3 của chương trình Toán 11 tập 1 tập trung vào các kiến thức quan trọng về hàm số và đồ thị. Bài viết này sẽ giúp bạn hiểu rõ hơn về cách giải các bài tập trong mục này, từ đó nâng cao kết quả học tập.
Hoàn thành bảng giá trị sau đây:
Hoạt động 4
Hoàn thành bảng giá trị sau đây:

Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
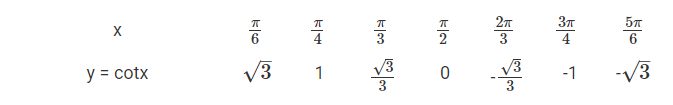
Hoạt động 5
Hoàn thành bảng giá trị sau đây:

Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
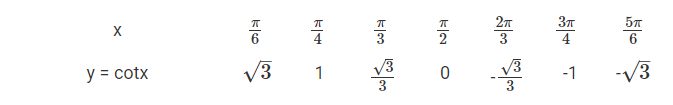
Thực hành 3
Li độ s (cm) của một con lắc đồng hộ theo thời gian t (giây) được cho bởi hàm số \(s = 2\cos \pi t\). Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 1 giây đầu thì li độ s nằm trong đoạn \(\left[ { - 1;1} \right]\,\,(cm)\).

Phương pháp giải:
Dựa vào đồ thị hàm côsin để giải quyết.
Lời giải chi tiết:
Ta có: \(s \in \left[ { - 1;1} \right]\, \Leftrightarrow - 1 \le 2\cos \pi t \le 1\)
\( \Leftrightarrow - \frac{1}{2} \le \cos \pi t \le \frac{1}{2}\)
Trong 1 giây đầu tiên \(0 < t < 1\) \( \Rightarrow 0 < \pi t < \pi \).
Đồ thị hàm số \(y = cosx\) trên \(\left[ {0;\pi } \right]\):
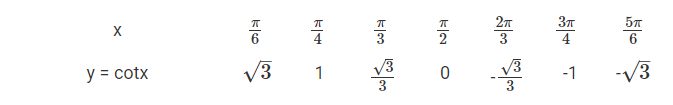
Dựa vào đồ thị ta thấy \( - \frac{1}{2} \le \cos \pi t \le \frac{1}{2} \Leftrightarrow \frac{\pi }{3} \le \pi t \le \frac{{2\pi }}{3} \Leftrightarrow \frac{1}{3} \le t \le \frac{2}{3}\)
Vậy \(t \in \left[ {\frac{1}{3};\frac{2}{3}} \right]\,\).
Hoạt động 6
Hoàn thành bảng giá trị sau đây:

Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
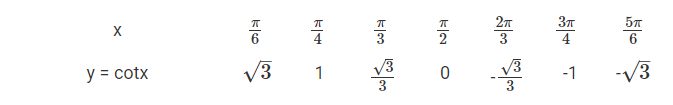
Hoạt động 7
Hoàn thành bảng giá trị sau đây:

Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
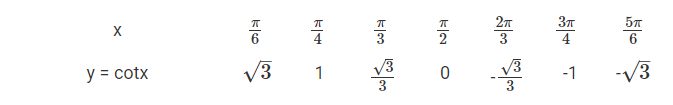
Thực hành 4
Có bao nhiêu giá trị x trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\) thỏa mãn điều kiện \(\tan x = 2\)?
Phương pháp giải:
Dựa vào đồ thị.
Lời giải chi tiết:

Từ đồ thị ta thấy có 4 giá trị x trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\) thỏa mãn điều kiện \(\tan x = 2\)
Hoạt động 3
Cho hàm số \(y = \cos x\) với \(x \in \left[ { - \frac{\pi }{2};\pi } \right]\).
a) Vẽ đồ thị hàm số đã cho.
b) Tại các điểm nào thì giá trị hàm số lớn nhất?
c) Tìm các giá trị của x thuộc \(\left[ {\frac{{ - \pi }}{4};\frac{{5\pi }}{4}} \right]\) sao cho \(\sin \left( {x - \frac{\pi }{4}} \right) < 0\).
Lời giải chi tiết:
a) Ta có đồ thị hàm số \(y = \cos x\) với \(x \in \left[ { - \frac{\pi }{2};\pi } \right]\) như hình dưới:

b) Tại điểm x =0 thì giá trị hàm số lớn nhất.
c) Do \(x \in \left[ {\frac{{ - \pi }}{4};\frac{{5\pi }}{4}} \right]\) nên \(\left( {x - \frac{\pi }{4}} \right) \in \left[ {\frac{{ - \pi }}{2};\pi } \right]\).
Để \(\sin \left( {x - \frac{\pi }{4}} \right) < 0\) thì \(\left( {x - \frac{\pi }{4}} \right) \in \left[ {\frac{{ - \pi }}{2};0} \right]\).
Suy ra \(x \in \left[ {\frac{{ - \pi }}{4};\frac{\pi }{4}} \right]\).
Vận dụng 2
Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong Hình 10. Trên bản đồ phẳng lấy đường xích đạo làm trục hoành và kinh tuyến \({0^o}\) làm trục tung. Khi đó tung độ của một điểm có vĩ độ \({\varphi ^o}\) \(( - {90^o} < \varphi < {90^o})\) được cho bởi hàm số \(y = 20\tan \left( {\frac{\pi }{{180}}\varphi } \right)\) (cm). Sử dụng đồ thị hàm số tang, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo 20cm trên bản đồ.
Phương pháp giải:
Vận dụng đồ thị của hàm số tan vào bài toán thực tế.
Lời giải chi tiết:
Ta có điểm nằm cách xích đạo 20cm có y = 20 hoặc y = - 20 nên \(\tan \left( {\frac{\pi }{{180}}\varphi } \right) = - 1\).
Vì \( - {90^o} < \varphi < {90^o}\) nên \( - \frac{\pi }{2} < \frac{\pi }{{180}}\varphi < \frac{\pi }{2}\).
Đặt \(x = \frac{\pi }{{180}}\varphi \) với \( - \frac{\pi }{2} < x < \frac{\pi }{2}\). Ta có đồ thị:

Từ đồ thị, ta có:
y = 1 khi \(x = \frac{\pi }{4} \Leftrightarrow \frac{\pi }{{180}}\varphi = \frac{\pi }{4} \Leftrightarrow \varphi = {45^o}\).
y = -1 khi \(x = - \frac{\pi }{4} \Leftrightarrow \frac{\pi }{{180}}\varphi = - \frac{\pi }{4} \Leftrightarrow \varphi = - {45^o}\).
Vậy trên bản đồ, các điểm nằm ở vĩ độ \({45^o}\) Bắc và \({45^o}\) Nam nằm cách xích đạo 20 cm.
Giải mục 3 trang 28, 29, 30, 31, 32 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 3 trong SGK Toán 11 tập 1 Chân trời sáng tạo là một phần quan trọng, đặt nền móng cho việc hiểu sâu hơn về các khái niệm hàm số bậc hai và ứng dụng của chúng. Nội dung này bao gồm các bài tập rèn luyện kỹ năng xác định, vẽ đồ thị hàm số bậc hai, tìm tọa độ đỉnh, trục đối xứng, và các điểm đặc biệt khác. Việc nắm vững kiến thức này không chỉ giúp bạn giải quyết các bài tập trong sách giáo khoa mà còn là cơ sở cho các kiến thức nâng cao hơn trong chương trình học.
Nội dung chính của Mục 3
- Bài 1 (Trang 28): Xác định các hệ số a, b, c của hàm số bậc hai và xác định hàm số có dạng y = ax2 + bx + c.
- Bài 2 (Trang 29): Tìm tọa độ đỉnh của parabol và vẽ đồ thị hàm số bậc hai.
- Bài 3 (Trang 30): Xác định trục đối xứng của parabol.
- Bài 4 (Trang 31): Tìm giao điểm của đồ thị hàm số với trục hoành (nếu có).
- Bài 5 (Trang 32): Ứng dụng đồ thị hàm số bậc hai để giải các bài toán thực tế.
Giải chi tiết các bài tập
Bài 1 (Trang 28)
Để xác định các hệ số a, b, c của hàm số bậc hai, bạn cần đưa hàm số về dạng y = ax2 + bx + c. Ví dụ, với hàm số y = 2x2 - 5x + 3, ta có a = 2, b = -5, c = 3.
Bài 2 (Trang 29)
Tọa độ đỉnh của parabol y = ax2 + bx + c được tính bằng công thức:
- xđỉnh = -b / (2a)
- yđỉnh = -Δ / (4a) (với Δ = b2 - 4ac)
Sau khi tính được tọa độ đỉnh, bạn có thể vẽ đồ thị hàm số bằng cách xác định thêm một vài điểm thuộc đồ thị và nối chúng lại với nhau.
Bài 3 (Trang 30)
Trục đối xứng của parabol là đường thẳng có phương trình x = -b / (2a). Đường thẳng này đi qua đỉnh của parabol và chia parabol thành hai phần đối xứng nhau.
Bài 4 (Trang 31)
Để tìm giao điểm của đồ thị hàm số với trục hoành, bạn cần giải phương trình ax2 + bx + c = 0. Nếu phương trình có nghiệm, thì đồ thị hàm số sẽ cắt trục hoành tại các điểm có hoành độ là nghiệm của phương trình.
Bài 5 (Trang 32)
Các bài toán ứng dụng thường yêu cầu bạn sử dụng đồ thị hàm số bậc hai để mô tả một tình huống thực tế và tìm ra các giá trị cần thiết. Ví dụ, bạn có thể sử dụng đồ thị hàm số để tìm chiều cao tối đa của một vật được ném lên không trung.
Lời khuyên khi học và giải bài tập
- Nắm vững lý thuyết: Hiểu rõ các khái niệm và công thức liên quan đến hàm số bậc hai.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Sử dụng công cụ hỗ trợ: Sử dụng máy tính bỏ túi hoặc các phần mềm vẽ đồ thị để kiểm tra kết quả và trực quan hóa hàm số.
- Tham khảo các nguồn tài liệu khác: Đọc thêm sách tham khảo, xem video bài giảng, hoặc tìm kiếm trên internet để hiểu sâu hơn về chủ đề này.
Hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn khi giải các bài tập trong Mục 3 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc bạn học tập tốt!