Bài 4 trang 70 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 4 trang 70 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài 4 trang 70 SGK Toán 11 Tập 1 thuộc chương trình Toán 11 Chân trời sáng tạo, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các khái niệm về tập xác định, tập giá trị, tính đơn điệu và cực trị của hàm số.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán hiệu quả.
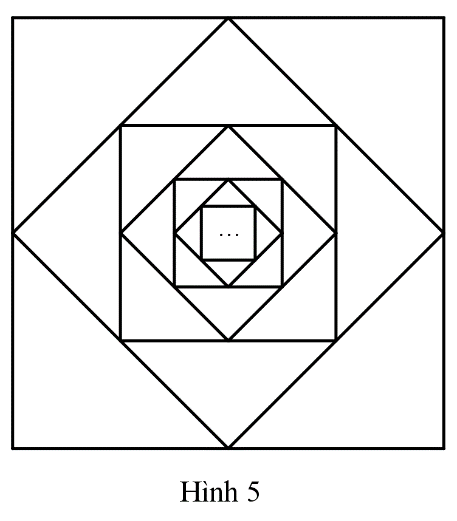
Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).
Đề bài
Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).
a) Kí hiệu \({a_n}\) là diện tích của hình vuông thứ \(n\) và \({S_n}\) là tổng diện tích của \(n\) hình vuông đầu tiên. Viết công thức tính \({a_n},{S_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {S_n}\) (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).
b) Kí hiệu \({p_n}\) là chu vi của hình vuông thứ \(n\) và \({Q_n}\) là tổng chu vi của \(n\) hình vuông đầu tiên. Viết công thức tính \({p_n}\) và \({Q_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {Q_n}\) (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).
Phương pháp giải - Xem chi tiết
Bước 1:Tìm cạnh của hình vuông thứ \(n\) dựa vào cạnh của hình vuông thứ \(n - 1\).
Bước 2: Tính chu vi và diện tích của hình vuông thứ \(n\).
Bước 3: Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\):
\(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết
a) Gọi \({u_n}\) là độ dài cạnh của hình vuông thứ n.
Đường chéo của hình vuông thứ n có độ dài là \({u_n}\sqrt 2 \).
Độ dài cạnh hình vuông thứ n + 1 bằng nửa độ dài đường chéo hình vuông thứ n nên ta có:
\({u_{n + 1}} = \frac{{{u_n}\sqrt 2 }}{2} = {u_n}.\frac{1}{{\sqrt 2 }}\).
Từ đó ta thấy \(\left( {{u_n}} \right)\) là một cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \({u_n} = {u_1}.{q^{n - 1}} = 1.{\left( {\frac{1}{{\sqrt 2 }}} \right)^{n - 1}} = \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Diện tích của hình vuông thứ \(n\) là: \({a_n} = u_n^2 = {\left( {\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)^2} = \frac{1}{{{2^{n - 1}}}},n = 1,2,3,...\)
Vậy \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}}\)
Đây là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{2}\).
Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = 2\left( {1 - \frac{1}{{{2^n}}}} \right)\).
\(\lim {S_n} = \lim 2\left( {1 - \frac{1}{{{2^n}}}} \right) = 2\left( {1 - \lim \frac{1}{{{2^n}}}} \right) = 2\left( {1 - 0} \right) = 2\).
b) Chu vi của hình vuông thứ \(n\) là: \({p_n} = 4{u_n} = 4.\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Vậy \({Q_n} = 4 + \frac{4}{{\sqrt 2 }} + \frac{4}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 4\left( {1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)\)
\(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}\) là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 1.\frac{{1 - {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^n}}}{{1 - \frac{1}{{\sqrt 2 }}}} = \left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\).
\( \Rightarrow {Q_n} = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\)
\(\begin{array}{l}\lim {Q_n} = \lim 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right) = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \lim \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\\ = 4\left( {2 + \sqrt 2 } \right)\left( {1 - 0} \right) = 4\left( {2 + \sqrt 2 } \right)\end{array}\).
Bài 4 trang 70 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 4 trang 70 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về hàm số bậc hai và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài tập yêu cầu xác định tập xác định của hàm số và tìm các điểm mà hàm số đạt giá trị lớn nhất hoặc nhỏ nhất. Cụ thể, bài tập có thể đưa ra một hàm số bậc hai và yêu cầu học sinh phân tích các yếu tố của hàm số để tìm ra tập xác định và các điểm cực trị.
Lời giải chi tiết
Để giải bài tập này, học sinh cần thực hiện các bước sau:
- Xác định tập xác định: Tập xác định của hàm số là tập hợp tất cả các giá trị của x mà tại đó hàm số có nghĩa. Đối với hàm số bậc hai, tập xác định thường là tập số thực R.
- Tìm điểm cực trị: Điểm cực trị của hàm số là điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất. Để tìm điểm cực trị, học sinh có thể sử dụng phương pháp đạo hàm hoặc phương pháp hoàn thiện bình phương.
- Xác định giá trị lớn nhất và nhỏ nhất: Sau khi tìm được điểm cực trị, học sinh có thể xác định giá trị lớn nhất và nhỏ nhất của hàm số bằng cách thay giá trị của x tại điểm cực trị vào hàm số.
Ví dụ minh họa
Giả sử hàm số được cho là: f(x) = -x2 + 4x - 3
- Tập xác định: Tập xác định của hàm số là R.
- Tìm điểm cực trị: Đạo hàm của hàm số là f'(x) = -2x + 4. Giải phương trình f'(x) = 0, ta được x = 2.
- Xác định giá trị lớn nhất và nhỏ nhất: Thay x = 2 vào hàm số, ta được f(2) = -22 + 4(2) - 3 = 1. Vì hệ số của x2 là âm, hàm số đạt giá trị lớn nhất tại x = 2 và giá trị lớn nhất là 1.
Lưu ý quan trọng
Khi giải bài tập về hàm số, học sinh cần chú ý đến các yếu tố sau:
- Tập xác định: Xác định đúng tập xác định của hàm số là bước quan trọng để đảm bảo tính chính xác của lời giải.
- Đạo hàm: Sử dụng đúng quy tắc đạo hàm để tìm điểm cực trị.
- Kiểm tra điều kiện: Kiểm tra điều kiện của bài toán để đảm bảo rằng lời giải phù hợp với yêu cầu.
Bài tập tương tự
Để rèn luyện kỹ năng giải bài tập về hàm số, học sinh có thể tham khảo các bài tập tương tự sau:
- Bài 1 trang 70 SGK Toán 11 Tập 1 - Chân trời sáng tạo
- Bài 2 trang 71 SGK Toán 11 Tập 1 - Chân trời sáng tạo
- Bài 3 trang 72 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Kết luận
Bài 4 trang 70 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và ứng dụng của nó. Bằng cách thực hiện các bước giải chi tiết và lưu ý các yếu tố quan trọng, học sinh có thể giải quyết bài tập này một cách hiệu quả.
tusach.vn hy vọng rằng lời giải chi tiết và hướng dẫn này sẽ giúp ích cho các bạn trong quá trình học tập!