Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 6 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài 6 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo là bài tập thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về phép biến hóa affine. Bài tập này yêu cầu học sinh phải hiểu rõ định nghĩa, tính chất và cách xác định phép biến hóa affine.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chứng minh rằng tam giác ABC, ta có (sin A = sin B.cos C + sin C.cos B)
Đề bài
Chứng minh rằng tam giác ABC, ta có \(\sin A = \sin B.\cos C + \sin C.\cos B\)
Phương pháp giải - Xem chi tiết
Sử dụng định lý tổng 3 góc trong một tam giác bằng 1800 và áp dụng công thức cộng.
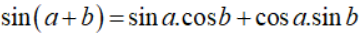
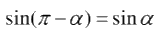
Lời giải chi tiết
Ta có: \(A + B + C = {180^0}\) (tổng 3 góc trong một tam giác)
\(\begin{array}{l} \Rightarrow A = {180^0} - \left( {B + C} \right)\\ \Leftrightarrow \sin A = \sin \left( {{{180}^0} - \left( {B + C} \right)} \right)\\ \Leftrightarrow \sin A = \sin \left( {B + C} \right) = \sin B.\cos C + \sin C.\cos B\end{array}\)
Bài 6 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 6 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về phép biến hóa affine. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 6 yêu cầu học sinh xác định một phép biến hóa affine dựa trên các thông tin cho trước. Thông thường, bài tập sẽ cung cấp các điểm ảnh hưởng và ảnh của chúng sau phép biến hóa, từ đó học sinh cần tìm ra ma trận biểu diễn của phép biến hóa affine đó.
Phương pháp giải
Để giải bài tập này, học sinh cần nắm vững các bước sau:
- Xác định các điểm ảnh hưởng: Tìm các điểm mà phép biến hóa biến đổi.
- Xác định ảnh của các điểm ảnh hưởng: Xác định vị trí mới của các điểm sau khi áp dụng phép biến hóa.
- Lập hệ phương trình: Sử dụng các điểm ảnh hưởng và ảnh của chúng để lập hệ phương trình tuyến tính.
- Giải hệ phương trình: Giải hệ phương trình để tìm ra các hệ số của ma trận biểu diễn phép biến hóa affine.
- Kiểm tra lại: Thay các hệ số tìm được vào ma trận và kiểm tra xem phép biến hóa có đúng với các điểm đã cho hay không.
Ví dụ minh họa
Giả sử chúng ta có một phép biến hóa affine f biến điểm A(1, 2) thành A'(3, 4) và điểm B(0, 1) thành B'(2, 3). Chúng ta cần tìm ma trận biểu diễn của phép biến hóa f.
Bước 1: Các điểm ảnh hưởng là A(1, 2) và B(0, 1).
Bước 2: Ảnh của các điểm ảnh hưởng là A'(3, 4) và B'(2, 3).
Bước 3: Giả sử ma trận biểu diễn của phép biến hóa f là:
a b c a11 a12 b1 a21 a22 b2
Khi đó, ta có:
- f(A) = A' => (a11 * 1 + a12 * 2 + b1, a21 * 1 + a22 * 2 + b2) = (3, 4)
- f(B) = B' => (a11 * 0 + a12 * 1 + b1, a21 * 0 + a22 * 1 + b2) = (2, 3)
Từ đó, ta có hệ phương trình:
- a11 + 2a12 + b1 = 3
- a21 + 2a22 + b2 = 4
- a12 + b1 = 2
- a22 + b2 = 3
Bước 4: Giải hệ phương trình này, ta tìm được các giá trị của a11, a12, a21, a22, b1, b2.
Bước 5: Thay các giá trị tìm được vào ma trận và kiểm tra lại.
Lưu ý khi giải bài tập
- Đảm bảo hiểu rõ định nghĩa và tính chất của phép biến hóa affine.
- Sử dụng đúng công thức và phương pháp giải.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh sẽ tự tin giải Bài 6 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo và đạt kết quả tốt trong môn học Toán 11.