Giải mục 1 trang 65 SGK Toán 11 tập 2 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn! Tại đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho bài tập mục 1 trang 65 SGK Toán 11 tập 2, theo chương trình Chân trời sáng tạo. Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán.
Bài viết này sẽ trình bày đầy đủ các bước giải, phân tích kỹ lưỡng từng khía cạnh của bài toán, giúp bạn hiểu rõ bản chất và áp dụng vào các bài tập tương tự.
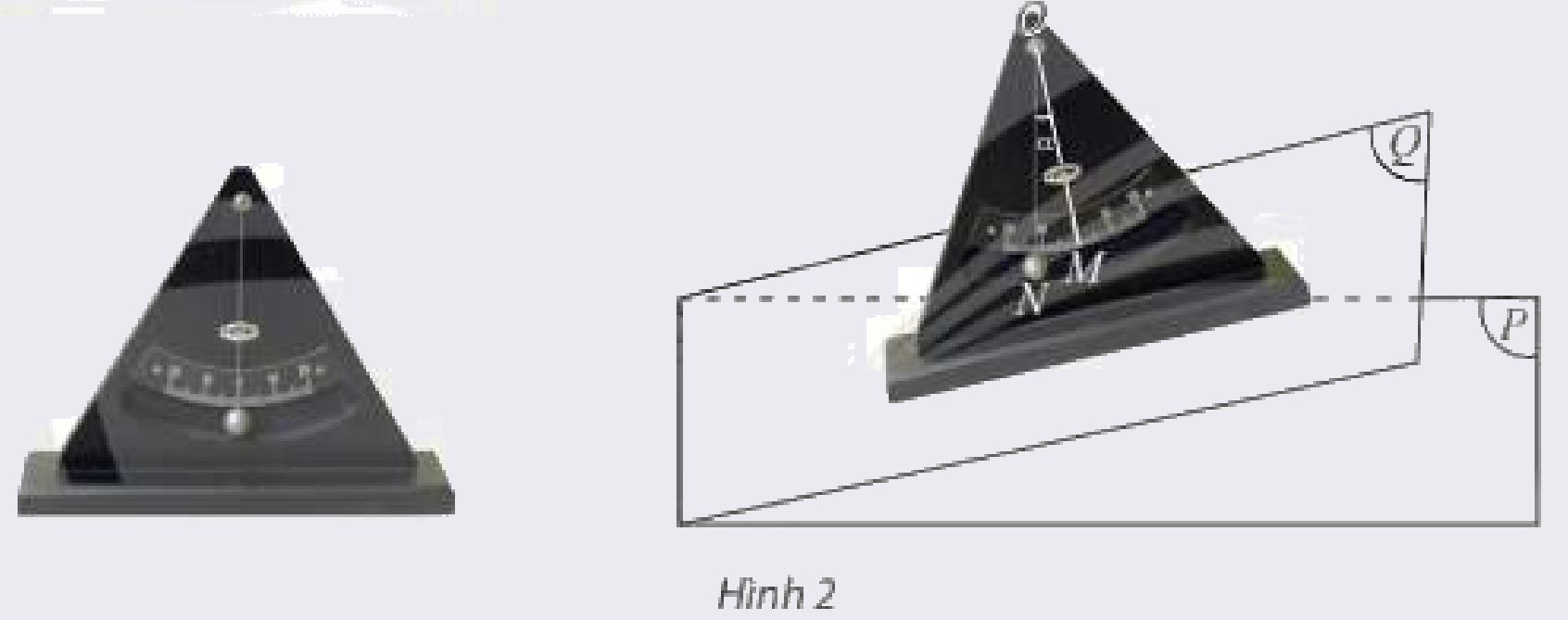
a) Có thể xác định góc giữa hai cánh của nắp hầm (Hình 1) bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh hay không?
Giải mục 1 trang 65 SGK Toán 11 tập 2 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 1 trang 65 SGK Toán 11 tập 2 Chân trời sáng tạo thường xoay quanh các bài toán về đạo hàm của hàm số. Đây là một phần kiến thức quan trọng trong chương trình Toán 11, đóng vai trò nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Bài viết này sẽ cung cấp hướng dẫn chi tiết, từng bước giải để giúp bạn hiểu rõ cách tiếp cận và giải quyết các bài toán này.
I. Tóm tắt lý thuyết cần nắm vững
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
- Đạo hàm của hàm số: Định nghĩa, ý nghĩa hình học và vật lý của đạo hàm.
- Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Đạo hàm của các hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
- Đạo hàm của hàm hợp: Quy tắc tính đạo hàm của hàm hợp.
II. Giải chi tiết bài tập mục 1 trang 65 SGK Toán 11 tập 2
Để minh họa, chúng ta sẽ cùng giải một bài tập cụ thể trong mục 1 trang 65. Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
- Bước 1: Áp dụng quy tắc tính đạo hàm của tổng và hiệu.
- Bước 2: Áp dụng quy tắc tính đạo hàm của hàm số lũy thừa.
- Bước 3: Tính đạo hàm của từng thành phần.
- Bước 4: Kết hợp các kết quả lại để có đạo hàm của hàm số f(x).
Kết quả: f'(x) = 3x2 + 4x - 5.
III. Các dạng bài tập thường gặp và phương pháp giải
Trong mục 1 trang 65, bạn có thể gặp các dạng bài tập sau:
- Tính đạo hàm của hàm số đơn giản: Sử dụng các quy tắc tính đạo hàm cơ bản.
- Tính đạo hàm của hàm số phức tạp: Sử dụng quy tắc tính đạo hàm của hàm hợp và các quy tắc khác.
- Tìm đạo hàm cấp hai: Tính đạo hàm của đạo hàm cấp một.
- Ứng dụng đạo hàm để giải các bài toán liên quan đến cực trị của hàm số: Tìm điểm cực đại, cực tiểu của hàm số.
IV. Mẹo giải nhanh và hiệu quả
Để giải các bài tập về đạo hàm nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
- Nắm vững các quy tắc tính đạo hàm: Điều này giúp bạn áp dụng một cách linh hoạt và chính xác.
- Phân tích cấu trúc của hàm số: Xác định hàm số chính và hàm số bên trong để áp dụng quy tắc tính đạo hàm của hàm hợp.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là chính xác.
V. Luyện tập thêm
Để củng cố kiến thức và kỹ năng, bạn nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. tusach.vn cung cấp đầy đủ các bài giải chi tiết cho tất cả các bài tập trong SGK Toán 11 tập 2 Chân trời sáng tạo. Hãy truy cập website của chúng tôi để tham khảo!
| Bài tập | Lời giải |
|---|
| Bài 1 | Xem lời giải |
| Bài 2 | Xem lời giải |
Chúc bạn học tốt và đạt kết quả cao trong môn Toán!