Bài 9 trang 13 Toán 11 Tập 1 - Chân trời sáng tạo

Bài 9 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 9 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo

Bài 9 trang 13 Toán 11 Tập 1 thuộc chương Hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về điều kiện xác định của hàm số, tập giá trị, và các tính chất của hàm số bậc hai để giải quyết các bài toán cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

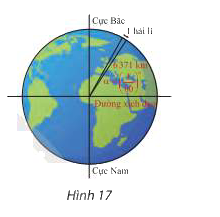
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = {\left( {\frac{1}{{60}}} \right)

Đề bài

Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = {\left( {\frac{1}{{60}}} \right)^\circ }\) của đường kinh tuyến (Hình 17). Đổi số đo \(\alpha \) sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilomet, biết bán kính trung bình của Trái Đất là 6371km. Làm tròn kết quả đến hàng phần trăm.

Bài 9 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiết Bài 9 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

Sử dụng công thức đổi độ sang rad : \({\alpha ^ \circ } = \frac{{\pi \alpha }}{{180}}\,\)rad

Và công thức tính chiều dài cung tròn \(l = \frac{{\pi R{n^ \circ }}}{{{{180}^ \circ }}}\) với R là bán kính và \({n^ \circ }\)là số đo góc của cung tròn

Lời giải chi tiết

Ta có \(\alpha = {\left( {\frac{1}{{60}}} \right)^\circ }\) suy ra \(\alpha = \frac{{\left( {\pi \frac{1}{{60}}} \right)}}{{180}} = \frac{\pi }{{10800}}\)

Một hải lí có độ dài bằng

\(l = \frac{{\pi R{n^ \circ }}}{{{{180}^ \circ }}} = \frac{{\pi .6371.{{\left( {\frac{1}{{60}}} \right)}^\circ }}}{{{{180}^ \circ }}} \approx 1,85\)(km)

Bài 9 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 9 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương Hàm số bậc hai, giúp học sinh củng cố kiến thức về tập xác định, tập giá trị và các tính chất của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài tập yêu cầu xác định tập xác định và tập giá trị của các hàm số sau:

y = √(2x - 1)
y = 1 / (x + 2)
y = x² - 4x + 3

Lời giải chi tiết

Câu a: y = √(2x - 1)

Để hàm số y = √(2x - 1) xác định, biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0:

2x - 1 ≥ 0

⇔ 2x ≥ 1

⇔ x ≥ 1/2

Vậy, tập xác định của hàm số là D = [1/2; +∞).

Vì √(2x - 1) ≥ 0 với mọi x ≥ 1/2, nên tập giá trị của hàm số là [0; +∞).

Câu b: y = 1 / (x + 2)

Để hàm số y = 1 / (x + 2) xác định, mẫu số phải khác 0:

x + 2 ≠ 0

⇔ x ≠ -2

Vậy, tập xác định của hàm số là D = R \ {-2}.

Hàm số có thể nhận mọi giá trị trừ 0. Do đó, tập giá trị của hàm số là R \ {0}.

Câu c: y = x² - 4x + 3

Hàm số y = x² - 4x + 3 là một hàm số bậc hai. Tập xác định của hàm số là D = R.

Để tìm tập giá trị, ta hoàn thiện bình phương:

y = x² - 4x + 4 - 4 + 3

y = (x - 2)² - 1

Vì (x - 2)² ≥ 0 với mọi x, nên y ≥ -1.

Vậy, tập giá trị của hàm số là [ -1; +∞).

Lưu ý quan trọng

Khi xác định tập xác định của hàm số, cần chú ý đến các điều kiện sau:
Mẫu số khác 0
Biểu thức dưới dấu căn lớn hơn hoặc bằng 0
Biểu thức trong logarit lớn hơn 0

Bài tập tương tự

Để rèn luyện thêm, các em có thể giải các bài tập tương tự sau:

Bài 10 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài tập ôn tập chương Hàm số bậc hai

Kết luận

Bài 9 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập cơ bản nhưng quan trọng, giúp học sinh hiểu rõ hơn về tập xác định và tập giá trị của hàm số. Việc nắm vững kiến thức này sẽ là nền tảng vững chắc cho các bài học tiếp theo.