Giải mục 4 trang 17, 18 , 19 GK Toán 11 tập 1 - Chân trời sáng tạo

Cho \(\alpha = \frac{\pi }{3}\). Biểu diễn các góc lượng giác \( - \alpha ,\alpha + \pi ,\pi - \alpha ,\frac{\pi }{2} - \alpha \) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc \(\alpha \)

Phương pháp giải:

Vẽ đường tròn lượng giác dựa vào kiến thức đã học rồi nhận xét

Lời giải chi tiết:

Dựa vào đường tròn lượng giác ta nhận được:

\(\left. \begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \end{array} \right\} \Rightarrow \left\{ \begin{array}{l}tan\left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array} \right.\)

\(\left. \begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array} \right.\)

\(\begin{array}{l}\left. \begin{array}{l}\sin \left( {\pi - \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\pi - \frac{\pi }{3}} \right) = - \frac{1}{2},\,\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\sin \left( {\pi - \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\\\cos \left( {\pi - \frac{\pi }{3}} \right) = - \cos \frac{\pi }{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)

\(\begin{array}{l}\left. \begin{array}{l}\sin \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \frac{1}{2},\,\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\sin \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \cos \frac{\pi }{3}\\\cos \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array} \right.\end{array}\)

a) Biểu diễn \(\cos 638^\circ \) qua gí trị lượng giác của góc có số đo từ \(0^\circ \) đến \(45^\circ \)

b) Biểu diễn \(\cot \frac{{19\pi }}{5}\) qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\)

Phương pháp giải:

Dựa vào ví dụ 4 để làm bài

Lời giải chi tiết:

a) \(\cos 638^\circ = \cos \left( {4.180^\circ + 90^\circ - 8^\circ } \right) = - \cos \left( {90^\circ - 8^\circ } \right) = - \sin 8^\circ \)

b) \(\cot \left( {\frac{{19\pi }}{5}} \right) = \cot \left( {4\pi - \frac{\pi }{5}} \right) = - \cot \left( {\frac{\pi }{5}} \right)\)

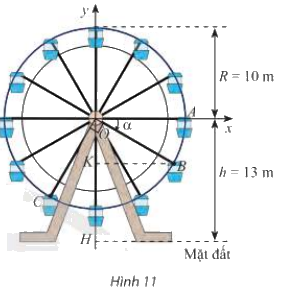
Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu với điểm B và C.

a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng \(\left( {13 + 10\sin \alpha } \right)\) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi \(\alpha = - 30^\circ \)

b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.

Phương pháp giải:

Dựa vào kiến thức lượng giác đã học để tính.

Lời giải chi tiết:

a) Chiều cao từ điểm B đến mặt đất là độ dài đoạn KH.

Điểm B là điểm biểu diễn cho góc lượng giác có số đo góc là \(\alpha \) trên đường tròn lượng giác có bán kính bằng 10 nên tọa độ điểm \(B(10\cos \alpha ;10\sin \alpha )\).

Vì tung độ điểm B có giá trị âm nên \(10\sin \alpha < 0\), suy ra độ dài \(OH = \left| {10\sin \alpha } \right| = - 10\sin \alpha \).

Ta có \(KH = OH - OK = 13 - ( - 10\sin \alpha ) = 13 + 10\sin \alpha \) (mét).

Với \(\alpha = - 30^\circ \Rightarrow KH = 13 + 10.\sin \left( { - 30^\circ } \right) = 8\,\,\left( m \right)\).

b) Nếu B cách mặt đất 4m \( \Rightarrow 4 = 13 + 10\sin \alpha \Leftrightarrow \sin \alpha = - \frac{9}{{10}}\).

Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\left( { - \frac{9}{{10}}} \right)^2} + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = - \frac{{\sqrt {19} }}{{10}}\).

Gọi M là hình chiếu của C lên OH.

\( \Rightarrow \cos \left( {\widehat {COH}} \right) = \sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha = - \frac{{\sqrt {19} }}{{10}}\).

Mà \(\cos \widehat {COH} = \frac{{OM}}{{OC}} \Rightarrow - \frac{{\sqrt {19} }}{{10}} = \frac{{OM}}{{OC}} \Rightarrow OM \approx 4,36\,\,\left( m \right)\).

\(\Rightarrow MH = OH - OM = h - OM = 13 - 4,36 = 8,64 m \).

Vậy điểm C cách mặt đất 8,64 m.