Giải mục 4 trang 83, 84 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 4 trang 83, 84 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài tập mục 4 trang 83, 84 SGK Toán 11 tập 1 - Chân trời sáng tạo trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho học sinh, tusach.vn đã biên soạn và trình bày lời giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các giải thích chi tiết và ví dụ minh họa.
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
Hoạt động 4
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
Hàm số \(y = f\left( x \right) + g\left( x \right)\) có liên tục tại \(x = 2\) không? Giải thích.
Phương pháp giải:
Xét tính liên tục của hàm số \(h\left( x \right) = f\left( x \right) + g\left( x \right)\) tại \(x = 2\):
Bước 1: Kiểm tra x = 2 có thuộc tập xác định không. Tính \(h\left( 2 \right)\).
Bước 2: Tính \(\mathop {\lim }\limits_{x \to 2} h\left( x \right)\).
Bước 3: Kết luận.
Lời giải chi tiết:
Đặt \(h\left( x \right) = f\left( x \right) + g\left( x \right) = \frac{1}{{x - 1}} + \sqrt {4 - x} \). Ta có:
\(\begin{array}{l}h\left( 2 \right) = \frac{1}{{2 - 1}} + \sqrt {4 - 2} = 1 + \sqrt 2 \\\mathop {\lim }\limits_{x \to 2} h\left( x \right) = \mathop {\lim }\limits_{x \to x} \left( {\frac{1}{{x - 1}} + \sqrt {4 - x} } \right) = \frac{1}{{2 - 1}} + \sqrt {4 - 2} = 1 + \sqrt 2 \end{array}\)
Vì \(\mathop {\lim }\limits_{x \to 2} h\left( x \right) = h\left( 2 \right)\) nên hàm số \(y = f\left( x \right) + g\left( x \right)\) liên tục tại \(x = 2\).
Thực hành 4
Xét tính liên tục của các hàm số:
a) \(y = \sqrt {{x^2} + 1} + 3 - x\);
b) \(y = \frac{{{x^2} - 1}}{x}.\cos x\).
Phương pháp giải:
Đưa hàm số thành tổng, hiệu, tích của hai hàm số rồi xét tính liên tục của hai hàm số đó.
Lời giải chi tiết:
a) TXĐ: \(D = \mathbb{R}\)
Hàm số \(y = \sqrt {{x^2} + 1} \) xác định trên \(\mathbb{R}\) nên liên tục trên \(\mathbb{R}\).
Hàm số \(y = 3 - x\) là đa thức nên liên tục trên \(\mathbb{R}\).
Vậy hàm số \(y = \sqrt {{x^2} + 1} + 3 - x\) cũng liên tục trên \(\mathbb{R}\).
b) TXĐ: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Hàm số \(y = \frac{{{x^2} - 1}}{x}\) là hàm phân thức hữu tỉ nên liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Hàm số \(y = \cos x\) là hàm lượng giác nên liên tục trên \(\mathbb{R}\). Vậy hàm số \(y = \cos x\) cũng liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Vậy hàm số \(y = \frac{{{x^2} - 1}}{x}.\cos x\) liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Vận dụng 3
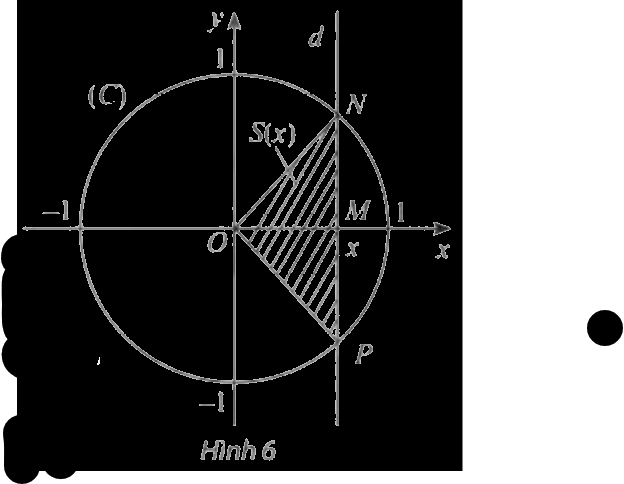
Trong mặt phẳng toạ độ \(Oxy\), cho đường tròn \(\left( C \right)\) tâm \(O\), bán kính bằng 1. Một đường thẳng \(d\) thay đổi, luôn vuông góc với trục hoành, cắt trục hoành tại điểm \(M\) có hoành độ \(x\left( { - 1 < x < 1} \right)\) và cắt đường tròn \(\left( C \right)\) tại các điểm \(N\) và \(P\) (xem Hình 6).
a) Viết biểu thức \(S\left( x \right)\) biểu thị diện tích của tam giác \(ONP\).
b) Hàm số \(y = S\left( x \right)\) có liên tục trên \(\left( { - 1;1} \right)\) không? Giải thích.
c) Tìm các giới hạn \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right)\) và \(\mathop {\lim }\limits_{x \to - {1^ + }} S\left( x \right)\).
Phương pháp giải:
a) Viết hàm số biểu thị phương trình đường tròn \(\left( C \right)\), dựa vào dữ kiện của đề bài, tính \(OM,NP\) sau đó tính diện tích \(S\left( x \right)\) của tam giác \(ONP\).
b) Sử dụng tính chất liên tục của các hàm số sơ cấp.
c) Áp dụng các công thức tính giới hạn của hàm số.
Lời giải chi tiết:
a) Ta có: \(\left( C \right):{x^2} + {y^2} = 1 \Leftrightarrow y = \pm \sqrt {1 - {x^2}} \).
Độ dài \(OM\) chính là giá trị tuyệt đối của hoành độ của điểm \(M\). Vậy \(OM = \left| x \right|\).
Độ dài \(MN\) chính là giá trị tuyệt đối của tung độ của điểm \(N\). Vậy \(MN = \left| {\sqrt {1 - {x^2}} } \right| = \sqrt {1 - {x^2}} \).
\(S\left( x \right) = {S_{ONP}} = \frac{1}{2}.NP.OM = MN.OM = \sqrt {1 - {x^2}} .\left| x \right|\).
b) Xét hàm số \(S\left( x \right) = \sqrt {1 - {x^2}} .\left| x \right| = \left\{ {\begin{array}{*{20}{c}}{x\sqrt {1 - {x^2}} }&{khi\,\,0 \le x \le 1}\\{ - x\sqrt {1 - {x^2}} }&{khi\,\, - 1 \le x < 0}\end{array}} \right.\).
ĐKXĐ: \(1 - {x^2} \ge 0 \Leftrightarrow - 1 \le x \le 1\)
Hàm số \(S\left( x \right)\) có tập xác định là \(\left[ { - 1;1} \right]\).
Vậy hàm số \(S\left( x \right)\) xác định trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\) nên liên tục trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\).
Ta có: \(S\left( 0 \right) = 0.\sqrt {1 - {0^2}} = 0\)
\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {x\sqrt {1 - {x^2}} } \right) = 0.\sqrt {1 - {0^2}} = 0\)
\(\mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x\sqrt {1 - {x^2}} } \right) = - 0.\sqrt {1 - {0^2}} = 0\)
Vì \(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = 0\) nên \(\mathop {\lim }\limits_{x \to 0} S\left( x \right) = 0 = S\left( 0 \right)\)
Vậy hàm số \(S\left( x \right)\) liên tục tại điểm \({x_0} = 0\). Vậy hàm số \(S\left( x \right)\) liên tục trên \(\left( { - 1;1} \right)\).
c) \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x\sqrt {1 - {x^2}} } \right) = 1.\sqrt {1 - {1^2}} = 0\)
\(\mathop {\lim }\limits_{x \to - {1^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( { - x\sqrt {1 - {x^2}} } \right) = - 1.\sqrt {1 - {{\left( { - 1} \right)}^2}} = 0\)
Giải mục 4 trang 83, 84 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 4 của SGK Toán 11 tập 1 - Chân trời sáng tạo tập trung vào việc nghiên cứu về đường thẳng trong không gian. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học tiếp theo, đặc biệt là hình học không gian. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết để đạt kết quả tốt trong môn Toán.
Nội dung chính của Mục 4
- Đường thẳng trong không gian: Định nghĩa, các dạng biểu diễn của đường thẳng trong không gian.
- Vị trí tương đối của hai đường thẳng trong không gian: Song song, cắt nhau, chéo nhau. Các điều kiện để xác định vị trí tương đối của hai đường thẳng.
- Góc giữa hai đường thẳng trong không gian: Định nghĩa, cách tính góc giữa hai đường thẳng.
- Khoảng cách giữa hai đường thẳng chéo nhau: Công thức tính khoảng cách giữa hai đường thẳng chéo nhau.
Giải chi tiết bài tập trang 83, 84 SGK Toán 11 tập 1 - Chân trời sáng tạo
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 4 trang 83, 84 SGK Toán 11 tập 1 - Chân trời sáng tạo:
Bài 1:
(Đề bài)
Lời giải:
(Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết)
Bài 2:
(Đề bài)
Lời giải:
(Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết)
Bài 3:
(Đề bài)
Lời giải:
(Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết)
Các dạng bài tập thường gặp và phương pháp giải
Trong quá trình ôn tập và làm bài tập về đường thẳng trong không gian, các bạn có thể gặp một số dạng bài tập sau:
- Xác định vị trí tương đối của hai đường thẳng: Sử dụng các điều kiện về vectơ chỉ phương và vectơ nối hai điểm thuộc hai đường thẳng.
- Tính góc giữa hai đường thẳng: Sử dụng công thức tính góc giữa hai vectơ.
- Tính khoảng cách giữa hai đường thẳng chéo nhau: Sử dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau.
- Chứng minh các tính chất liên quan đến đường thẳng trong không gian: Sử dụng các định lý và tính chất đã học.
Mẹo học tập hiệu quả
- Nắm vững các định nghĩa, định lý và công thức: Đây là nền tảng để giải quyết mọi bài tập.
- Vẽ hình minh họa: Hình vẽ giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Tham khảo các nguồn tài liệu khác: Sách tham khảo, bài giảng trực tuyến, video hướng dẫn... có thể cung cấp cho bạn những kiến thức bổ ích.
Kết luận
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các bạn học sinh đã có thể tự tin giải quyết các bài tập trong mục 4 trang 83, 84 SGK Toán 11 tập 1 - Chân trời sáng tạo. Chúc các bạn học tập tốt và đạt kết quả cao trong môn Toán!
Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ nhé!