Đề bài
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(A'B'\) và \(O\) là một điểm thuộc miền trong của mặt bên \(CC'D'D\). Tìm giao tuyến của mặt phẳng \(\left( {OMN} \right)\) với các mặt của hình hộp.
Phương pháp giải - Xem chi tiết
Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:
+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.
+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.
Lời giải chi tiết
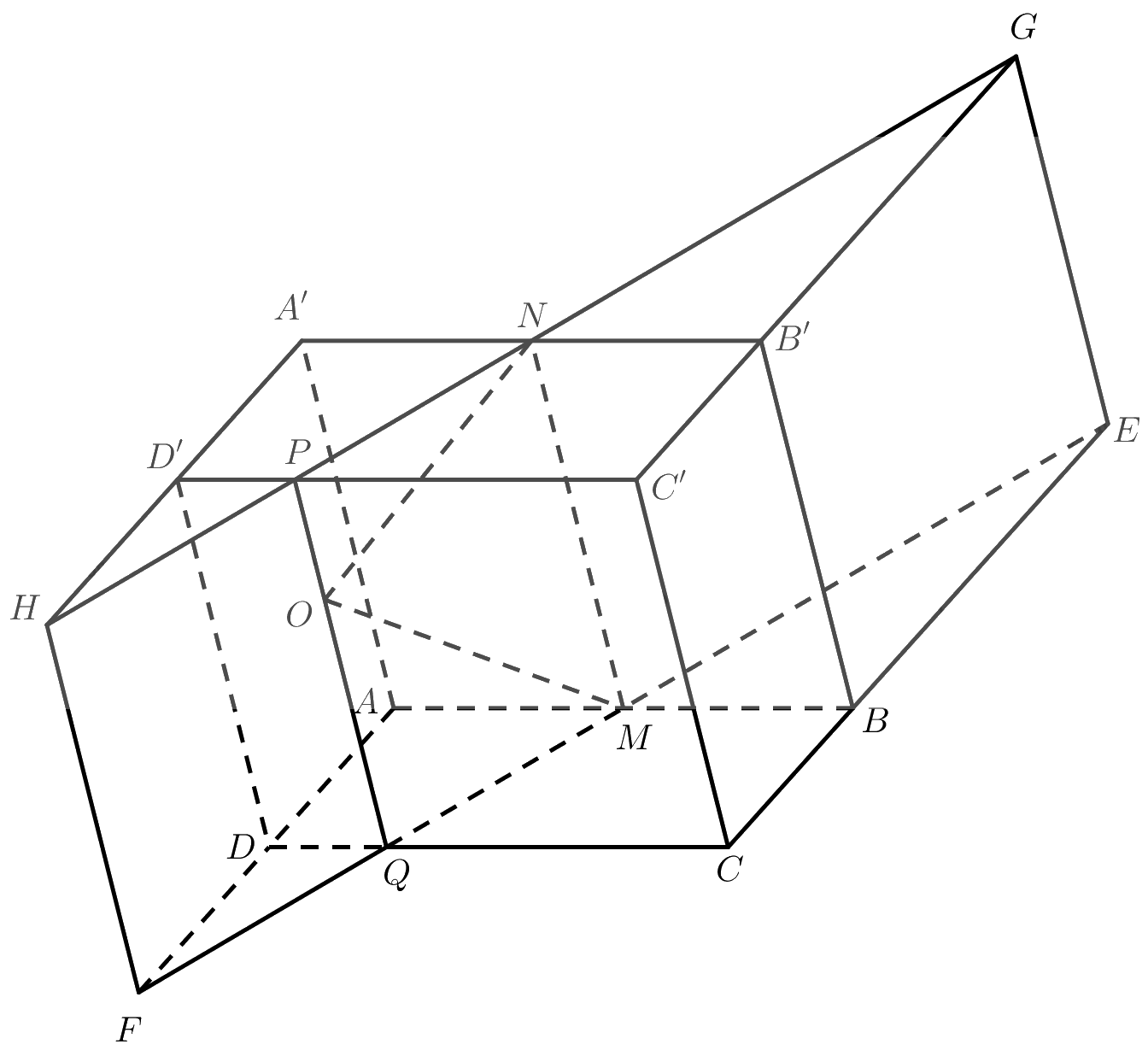
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in AB \subset \left( {ABB'A'} \right)\\M \in \left( {OMN} \right)\end{array} \right\} \Rightarrow M \in \left( {OMN} \right) \cap \left( {ABB'A'} \right)\\\left. \begin{array}{l}N \in A'B' \subset \left( {ABB'A'} \right)\\N \in \left( {OMN} \right)\end{array} \right\} \Rightarrow N \in \left( {OMN} \right) \cap \left( {ABB'A'} \right)\\ \Rightarrow \left( {OMN} \right) \cap \left( {ABB'A'} \right) = MN\end{array}\)
\(M\) là trung điểm của \(AB\)
\(N\) là trung điểm của \(A'B'\)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABB'A'\)
\( \Rightarrow MN\parallel AA'\parallel BB'\parallel CC'\parallel DD'\)
\(\left. \begin{array}{l}O \in \left( {OMN} \right) \cap \left( {C{\rm{DD'C'}}} \right)\\MN\parallel C{\rm{D}}\\MN \subset \left( {OMN} \right)\\C{\rm{D}} \subset \left( {C{\rm{DD'C'}}} \right)\end{array} \right\}\)
\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {C{\rm{DD'C'}}} \right)\) là đường thẳng \(d\) đi qua \(O\), song song với \(MN\) và \(C{\rm{D}}\).
Gọi \(P = d \cap C'D',Q = d \cap CD \Rightarrow \left( {OMN} \right) \cap \left( {C{\rm{DD'C'}}} \right) = PQ\)
\(\begin{array}{l}\left. \begin{array}{l}M \in AB \subset \left( {ABC{\rm{D}}} \right)\\M \in \left( {OMN} \right)\end{array} \right\} \Rightarrow M \in \left( {OMN} \right) \cap \left( {ABC{\rm{D}}} \right)\\\left. \begin{array}{l}Q \in C{\rm{D}} \subset \left( {ABC{\rm{D}}} \right)\\Q \in d \subset \left( {OMN} \right)\end{array} \right\} \Rightarrow Q \in \left( {OMN} \right) \cap \left( {ABC{\rm{D}}} \right)\\ \Rightarrow \left( {OMN} \right) \cap \left( {ABC{\rm{D}}} \right) = MQ\end{array}\)
\(\begin{array}{l}\left. \begin{array}{l}N \in A'B' \subset \left( {A'B'C'{\rm{D'}}} \right)\\N \in \left( {OMN} \right)\end{array} \right\} \Rightarrow N \in \left( {OMN} \right) \cap \left( {A'B'C'{\rm{D'}}} \right)\\\left. \begin{array}{l}P \in C'{\rm{D'}} \subset \left( {A'B'C'{\rm{D'}}} \right)\\P \in d \subset \left( {OMN} \right)\end{array} \right\} \Rightarrow P \in \left( {OMN} \right) \cap \left( {A'B'C'{\rm{D'}}} \right)\\ \Rightarrow \left( {OMN} \right) \cap \left( {A'B'C'{\rm{D'}}} \right) = NP\end{array}\)
Gọi \(E = MQ \cap BC,F = MQ \cap AD,G = NP \cap B'C',H = NP \cap A'D'\)
\(\begin{array}{l}\left. \begin{array}{l}E \in BC \subset \left( {BCC'B'} \right)\\E \in MQ \subset \left( {OMN} \right)\end{array} \right\} \Rightarrow E \in \left( {OMN} \right) \cap \left( {BCC'B'} \right)\\\left. \begin{array}{l}G \in B'C' \subset \left( {BCC'B'} \right)\\G \in NP \subset \left( {OMN} \right)\end{array} \right\} \Rightarrow G \in \left( {OMN} \right) \cap \left( {BCC'B'} \right)\\ \Rightarrow \left( {OMN} \right) \cap \left( {BCC'B'} \right) = EG\end{array}\)
\(\begin{array}{l}\left. \begin{array}{l}F \in A{\rm{D}} \subset \left( {A{\rm{DD'A'}}} \right)\\F \in MQ \subset \left( {OMN} \right)\end{array} \right\} \Rightarrow F \in \left( {OMN} \right) \cap \left( {A{\rm{DD'A'}}} \right)\\\left. \begin{array}{l}H \in A'D' \subset \left( {A{\rm{DD'A'}}} \right)\\H \in NP \subset \left( {OMN} \right)\end{array} \right\} \Rightarrow H \in \left( {OMN} \right) \cap \left( {A{\rm{DD'A'}}} \right)\\ \Rightarrow \left( {OMN} \right) \cap \left( {A{\rm{DD'A'}}} \right) = FH\end{array}\)
