Bài 3 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 3 trang 12 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài 3 trang 12 SGK Toán 11 Tập 1 - Chân trời sáng tạo là bài tập thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
Đề bài
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
a) \(\frac{{ - 17\pi }}{3}\)
b) \(\frac{{13\pi }}{4}\)
c) \( - 765^\circ \)
Phương pháp giải - Xem chi tiết
Biểu diễn dựa trên các góc đặc biệt
Lời giải chi tiết
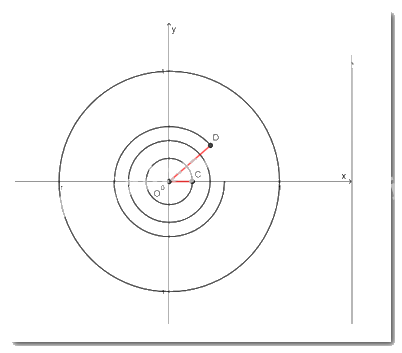
a) \(\frac{{ - 17\pi }}{3} = - 5\pi - \frac{{2\pi }}{3}\)
\( \Rightarrow \left( {OC,OD} \right) = \frac{{ - 17\pi }}{3}\)
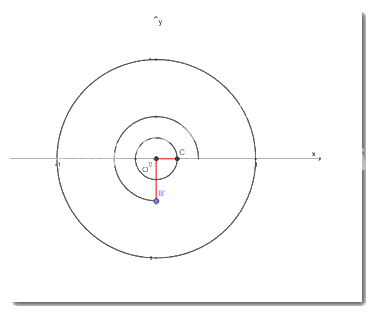
b) \(\frac{{13\pi }}{4} = 3\pi + \frac{\pi }{4}\)
\( \Rightarrow \left( {OC,OB'} \right) = \frac{{13\pi }}{4}\)
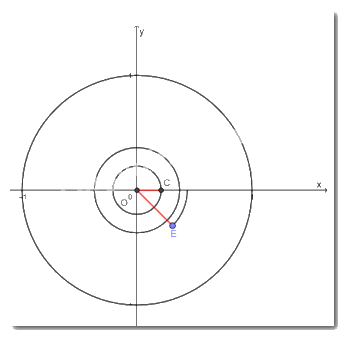
c) \( - 765^\circ = 2.\left( { - 360^\circ } \right) - 45^\circ \)
\( \Rightarrow \left( {OC;OE} \right) = - 765^\circ \)
Bài 3 trang 12 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 3 trang 12 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về giới hạn của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 3 yêu cầu tính các giới hạn sau:
- lim (x→2) (x² - 3x + 2) / (x - 2)
- lim (x→-1) (x³ + 1) / (x + 1)
- lim (x→0) (√(x+1) - 1) / x
Lời giải chi tiết
1. lim (x→2) (x² - 3x + 2) / (x - 2)
Ta có thể phân tích tử thức:
x² - 3x + 2 = (x - 1)(x - 2)
Vậy:
lim (x→2) (x² - 3x + 2) / (x - 2) = lim (x→2) (x - 1)(x - 2) / (x - 2) = lim (x→2) (x - 1) = 2 - 1 = 1
2. lim (x→-1) (x³ + 1) / (x + 1)
Ta có thể phân tích tử thức:
x³ + 1 = (x + 1)(x² - x + 1)
Vậy:
lim (x→-1) (x³ + 1) / (x + 1) = lim (x→-1) (x + 1)(x² - x + 1) / (x + 1) = lim (x→-1) (x² - x + 1) = (-1)² - (-1) + 1 = 1 + 1 + 1 = 3
3. lim (x→0) (√(x+1) - 1) / x
Để tính giới hạn này, ta có thể nhân cả tử và mẫu với liên hợp của tử thức:
lim (x→0) (√(x+1) - 1) / x = lim (x→0) [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)] = lim (x→0) (x + 1 - 1) / [x(√(x+1) + 1)] = lim (x→0) x / [x(√(x+1) + 1)] = lim (x→0) 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2
Lưu ý quan trọng
- Khi tính giới hạn, cần chú ý đến các dạng giới hạn cơ bản và các phương pháp như phân tích tử thức, nhân với liên hợp.
- Kiểm tra kỹ điều kiện xác định của biểu thức.
- Thực hành nhiều bài tập để nắm vững kiến thức và kỹ năng.
Ứng dụng của giới hạn hàm số
Giới hạn hàm số là một khái niệm nền tảng trong giải tích, có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau, bao gồm:
- Tính đạo hàm của hàm số.
- Tính tích phân của hàm số.
- Nghiên cứu sự biến thiên của hàm số.
- Giải các bài toán về tối ưu hóa.
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh có thể tự tin giải Bài 3 trang 12 SGK Toán 11 Tập 1 - Chân trời sáng tạo và các bài tập tương tự. Chúc các bạn học tốt!