Bài 11 Trang 128 Toán 11 Tập 1 - Chân Trời Sáng Tạo

Bài 11 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 11 thuộc chương trình Toán 11 tập 1, sách Chân trời sáng tạo, tập trung vào việc ôn tập chương 1: Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, tích vô hướng, và ứng dụng của vectơ để giải quyết các bài toán hình học.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

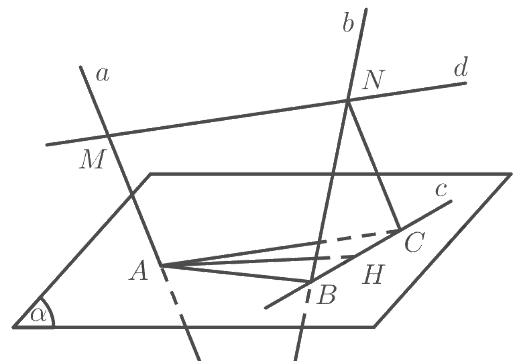
Cho mặt phẳng \(\left( \alpha \right)\) và hai đường thẳng chéo nhau \(a,b\) cắt \(\left( \alpha \right)\) tại \(A\) và \(B\). Gọi \(d\) là đường thẳng thay đổi luôn luôn song song với \(\left( \alpha \right)\) và cắt \(a\) tại \(M\), cắt \(b\) tại \(N\). Qua điểm \(N\) dựng đường thẳng song song với \(a\) cắt \(\left( \alpha \right)\) tại điểm \(C\).

Đề bài

a) Tứ giác \(MNCA\) là hình gì?

b) Chứng minh rằng điểm \(C\) luôn luôn chạy trên một đường thẳng cố định.

c) Xác định vị trí của đường thẳng \(d\) để độ dài \(MN\) nhỏ nhất.

Phương pháp giải - Xem chi tiết Bài 11 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

Sử dụng hệ quả: Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Lời giải chi tiết

Bài 11 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

a) Ta có:

\(\left. \begin{array}{l}d \subset \left( {AMNC} \right)\\d\parallel \left( \alpha \right)\\\left( \alpha \right) \cap \left( {AMNC} \right) = AC\end{array} \right\} \Rightarrow d\parallel AC \Rightarrow MN\parallel AC\)

Mà \(a\parallel NC \Rightarrow MA\parallel NC\)

\( \Rightarrow AMNC\) là hình bình hành.

b) Gọi \(\left( \beta \right)\) là mặt phẳng chứa \(b\) và song song với \(a\), \(c = \left( \alpha \right) \cap \left( \beta \right)\)

Ta có:

\(\left. \begin{array}{l}NC\parallel a\\N \in b\end{array} \right\} \Rightarrow NC \subset \left( \beta \right)\)

\( \Rightarrow C \in \left( \alpha \right) \cap \left( \beta \right) \Rightarrow C \in c\)

Vậy điểm \(C\) luôn luôn chạy trên đường thẳng \(c\) là giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) cố định.

c) Trong mặt phẳng \(\left( \alpha \right)\), kẻ \(AH \bot c\)

Vì \(c\) cố định nên \(AC \ge AH\)

\(AMNC\) là hình bình hành \( \Rightarrow MN = AC\)

Vậy \(MN \ge AH\)

Vậy \(MN\) nhỏ nhất khi \(C \equiv H\). Khi đó \(d\parallel AH\).

Bài 11 Trang 128 SGK Toán 11 Tập 1 - Chân Trời Sáng Tạo: Giải Chi Tiết và Hướng Dẫn

Bài 11 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình ôn tập chương 1 về vectơ. Bài tập này không chỉ giúp học sinh củng cố kiến thức đã học mà còn rèn luyện kỹ năng giải toán một cách linh hoạt và sáng tạo. Dưới đây là giải chi tiết bài 11, cùng với những hướng dẫn và lưu ý quan trọng để bạn có thể tự tin giải quyết bài toán này.

Nội dung bài tập

Bài 11 thường bao gồm các dạng bài tập sau:

Tính toán với vectơ: Thực hiện các phép cộng, trừ, nhân với một số thực vectơ.
Tích vô hướng của hai vectơ: Tính tích vô hướng, xác định góc giữa hai vectơ, kiểm tra tính vuông góc.
Ứng dụng của vectơ trong hình học: Chứng minh các đẳng thức vectơ, giải các bài toán liên quan đến tam giác, hình bình hành, và các hình khác.

Giải chi tiết bài 11 (Ví dụ minh họa)

(Giả sử bài 11 có nội dung cụ thể như sau: Cho tam giác ABC, với A(1;2), B(3;4), C(-1;0). Tính độ dài các cạnh của tam giác ABC và xác định loại tam giác này.)

Tính độ dài cạnh AB: Sử dụng công thức tính khoảng cách giữa hai điểm: AB = √((3-1)² + (4-2)²) = √(2² + 2²) = √8 = 2√2
Tính độ dài cạnh BC: BC = √((-1-3)² + (0-4)²) = √((-4)² + (-4)²) = √32 = 4√2
Tính độ dài cạnh AC: AC = √((-1-1)² + (0-2)²) = √((-2)² + (-2)²) = √8 = 2√2
Kết luận: Vì AB = AC = 2√2, tam giác ABC là tam giác cân tại A.

Mẹo giải bài tập vectơ hiệu quả

Nắm vững định nghĩa và tính chất của vectơ: Hiểu rõ các khái niệm cơ bản như vectơ, độ dài vectơ, tích vô hướng, và các tính chất liên quan.
Sử dụng hình vẽ: Vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
Biến đổi vectơ một cách linh hoạt: Sử dụng các quy tắc cộng, trừ, nhân vectơ để biến đổi biểu thức vectơ cho đơn giản.
Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Tài liệu tham khảo hữu ích

Ngoài SGK Toán 11 tập 1 - Chân trời sáng tạo, bạn có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 11
Các trang web học Toán trực tuyến uy tín như tusach.vn
Các video bài giảng trên YouTube

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập vectơ, bạn nên luyện tập thêm các bài tập tương tự trong SGK và sách bài tập. Hãy tìm kiếm các bài tập có độ khó tăng dần để thử thách bản thân và nâng cao khả năng giải toán.

tusach.vn hy vọng với những hướng dẫn chi tiết và hữu ích trên, bạn sẽ tự tin giải quyết Bài 11 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.

Bài 11 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 11 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 11 Trang 128 SGK Toán 11 Tập 1 - Chân Trời Sáng Tạo: Giải Chi Tiết và Hướng Dẫn

Nội dung bài tập

Giải chi tiết bài 11 (Ví dụ minh họa)

Mẹo giải bài tập vectơ hiệu quả

Tài liệu tham khảo hữu ích

Luyện tập thêm

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN