Giải mục 1 trang 19, 20, 21, 22 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 19, 20, 21, 22 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong mục 1 trang 19, 20, 21, 22 SGK Toán 11 tập 2 chương trình Chân trời sáng tạo. Chúng tôi giúp học sinh nắm vững kiến thức và tự tin giải các bài tập Toán 11.
Với đội ngũ giáo viên giàu kinh nghiệm, các lời giải của chúng tôi không chỉ cung cấp đáp án mà còn giải thích rõ ràng từng bước, giúp học sinh hiểu sâu sắc bản chất của bài toán.
Nguyên phân là quá trình tế bào phân chia thành hai tế bào con giống hệt nhau về mặt di truyền.
Hoạt động 1
Nguyên phân là quá trình tế bào phân chia thành hai tế bào con giống hệt nhau về mặt di truyền.
Lập bảng sau đây để tính số tế bào được tạo ra từ một tế bào ban đầu sau những lần nguyên phân.
a) Hoàn thành bảng trên vào vở.
b) Gọi \(y\) là số tế bào được tạo ra từ một tế bào ban đầu sau \(x\left( {x = 0,1,2,...} \right)\) lần nguyên phân. Viết công thức biểu thị \(y\) theo \(x\).
Phương pháp giải:
Tìm ra quy luật của dãy số sau đó điền vào bảng và biểu thị \(y\) theo \(x\).
Lời giải chi tiết:
a)
b) Với \(x = 0:y = 1 = {2^0}\)
Với \(x = 1:y = 2 = {2^1}\)
Với \(x = 2:y = 4 = {2^2}\)
Với \(x = 3:y = 8 = {2^3}\)
…
Với \(x = 7:y = 128 = {2^7}\)
Vậy \(y = {2^x}\).
Hoạt động 2
a) Xét hàm số mũ \(y = {2^x}\) với tập xác định \(\mathbb{R}\).

i) Hoàn thành bảng giá trị sau:

ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị hàm số \(y = {2^x}\) như Hình 2. Từ đồ thị nảy, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to - \infty \) và tập giá trị của hàm số đã cho.
b) Lập bảng giá trị và vẽ đồ thị của hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to - \infty \) và tập giá trị của hàm số này.
Phương pháp giải:
a) Thay các giá trị của \(x\) vào hàm số sau đó dựa vào đồ thị nhận xét.
b) Lập bảng giá trị, vẽ đồ thị hàm số, sau đó dựa vào đồ thị nhận xét.
Lời giải chi tiết:
a) i)

ii) ‒ Hàm số liên tục trên \(\mathbb{R}\).
‒ Hàm số đồng biến trên \(\mathbb{R}\).
‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {2^x} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } {2^x} = 0\).
‒ Tập giá trị: \(\left( {0; + \infty } \right)\).
b) Bảng giá trị:
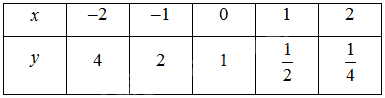
Đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\):
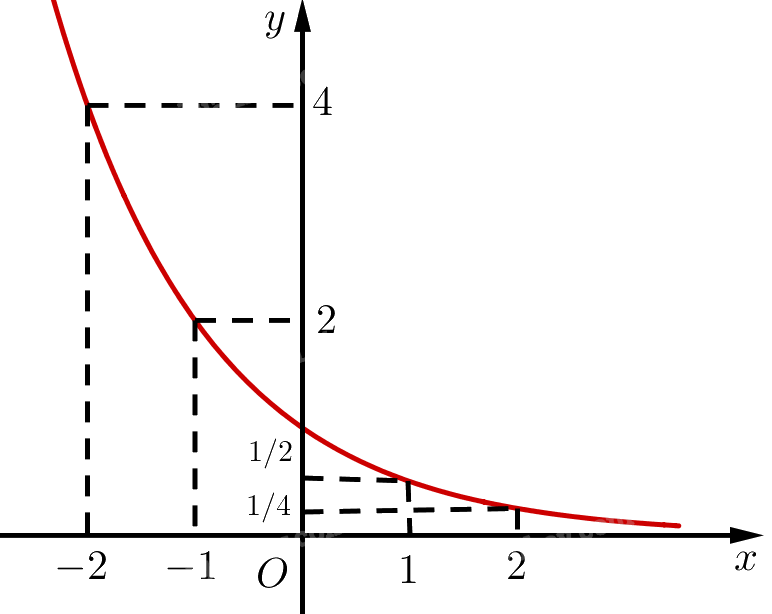
‒ Hàm số liên tục trên \(\mathbb{R}\).
‒ Hàm số nghịch biến trên \(\mathbb{R}\).
‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{2}} \right)^x} = 0;\mathop {\lim }\limits_{x \to - \infty } {\left( {\frac{1}{2}} \right)^x} = + \infty \).
‒ Tập giá trị: \(\left( {0; + \infty } \right)\).
Thực hành 1
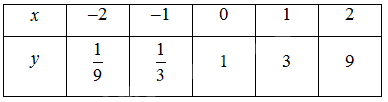
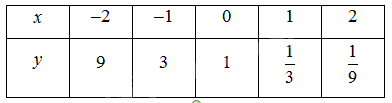
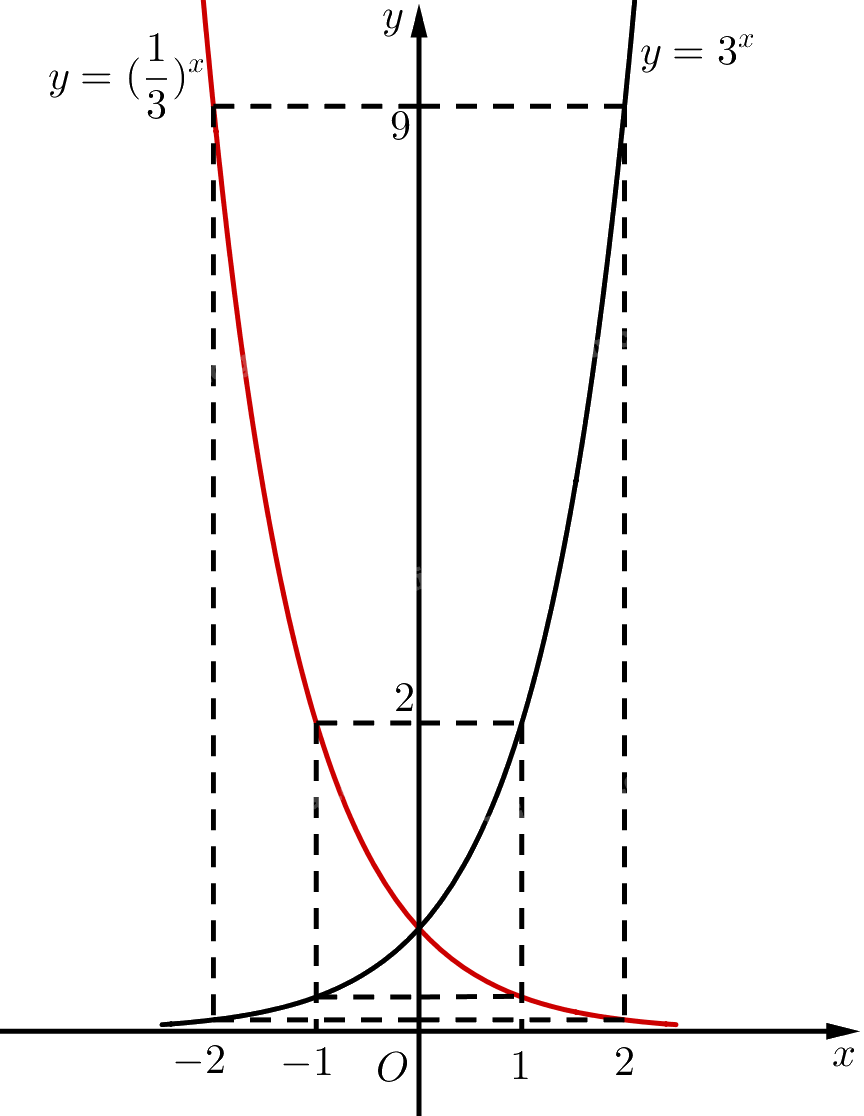
Trên cùng một hệ trục toạ độ, vẽ đồ thị các hàm số \(y = {3^x}\) và \(y = {\left( {\frac{1}{3}} \right)^x}\).
Phương pháp giải:
Lập bảng giá trị, dựa vào bảng giá trị vẽ đồ thị.
Lời giải chi tiết:
Bảng giá trị:
‒ Hàm số \(y = {3^x}\):

‒ Hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\):

‒ Đồ thị:

Thực hành 2
So sánh các cặp số sau:
a) \(0,{85^{0,1}}\) và \(0,{85^{ - 0,1}}\).
b) \({\pi ^{ - 1,4}}\) và \({\pi ^{ - 0,5}}\).
c) \(\sqrt[4]{3}\) và \(\frac{1}{{\sqrt[4]{3}}}\).
Phương pháp giải:
Sử dụng tính chất của hàm số mũ.
Lời giải chi tiết:
a) Do \(0,85 < 1\) nên hàm số \(y = 0,{85^x}\) nghịch biến trên \(\mathbb{R}\).
Mà \(0,1 > - 0,1\) nên \(0,{85^{0,1}} < 0,{85^{ - 0,1}}\).
b) Do \(\pi > 1\) nên hàm số \(y = {\pi ^x}\) đồng biến trên \(\mathbb{R}\).
Mà \( - 1,4 < - 0,5\) nên \({\pi ^{ - 1,4}} < {\pi ^{ - 0,5}}\).
c) \(\sqrt[4]{3} = {3^{\frac{1}{4}}};\frac{1}{{\sqrt[4]{3}}} = \frac{1}{{{3^{\frac{1}{4}}}}} = {3^{ - \frac{1}{4}}}\).
Do \(3 > 1\) nên hàm số \(y = {3^x}\) đồng biến trên \(\mathbb{R}\).
Mà \(\frac{1}{4} > - \frac{1}{4}\) nên \({3^{\frac{1}{4}}} > {3^{ - \frac{1}{4}}} \Leftrightarrow \sqrt[4]{3} > \frac{1}{{\sqrt[4]{3}}}\).
Vận dụng 1
Khối lượng vi khuẩn của một mẻ nuôi cấy sau \(t\) giờ kể từ thời điểm ban đầu được cho bởi công thức \(M\left( t \right) = 50.1,{06^t}\left( g \right)\).
(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, năm 2017, trang 101)
a) Tìm khối lượng vi khuẩn tại thời điểm bắt đầu nuôi cấy (gọi là khối lượng ban đầu).
b) Tính khối lượng vi khuẩn sau 2 giờ và sau 10 giờ (làm tròn kết quả đến hàng phần trăm).
c) Khối lượng vi khuẩn tăng dần hay giảm dần theo thời gian? Tại sao?
Phương pháp giải:
a) Thay \(t = 0\) vào công thức \(M\left( t \right)\).
b) Thay \(t = 2\) và \(t = 10\) vào công thức \(M\left( t \right)\).
c) Xét hàm số mũ \(M\left( t \right)\).
Lời giải chi tiết:
a) Khối lượng vi khuẩn tại thời điểm bắt đầu nuôi cấy là:
\(M\left( 0 \right) = 50.1,{06^0} = 50\left( g \right)\).
b) Khối lượng vi khuẩn sau 2 giờ là:
\(M\left( 2 \right) = 50.1,{06^2} = 56,18\left( g \right)\).
Khối lượng vi khuẩn sau 10 giờ là:
\(M\left( {10} \right) = 50.1,{06^{10}} \approx 89,54\left( g \right)\)
c) Xét hàm số \(M\left( t \right) = 50.1,{06^t}\).
Vì \(1,06 > 1\) nên hàm số \(M\left( t \right) = 50.1,{06^t}\) là hàm số đồng biến. Vậy khối lượng vi khuẩn tăng dần theo thời gian.
Giải mục 1 trang 19, 20, 21, 22 SGK Toán 11 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 1 của SGK Toán 11 tập 2 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng trong mục này là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương tiếp theo. Tusach.vn xin giới thiệu hướng dẫn giải chi tiết các bài tập trang 19, 20, 21, 22, giúp các em học sinh hiểu rõ hơn về nội dung bài học và rèn luyện kỹ năng giải toán.
Nội dung chính của Mục 1 (Trang 19-22)
Trước khi đi vào giải bài tập, chúng ta cần nắm vững nội dung chính của Mục 1. Thông thường, mục này sẽ giới thiệu về:
- Các khái niệm cơ bản liên quan đến chủ đề.
- Các định lý, tính chất quan trọng.
- Các ví dụ minh họa.
Việc hiểu rõ những kiến thức này sẽ giúp các em dễ dàng tiếp cận và giải quyết các bài tập một cách hiệu quả.
Giải chi tiết các bài tập trang 19, 20, 21, 22
Dưới đây là giải chi tiết các bài tập trong Mục 1, trang 19, 20, 21, 22 SGK Toán 11 tập 2 Chân trời sáng tạo:
Bài 1 (Trang 19)
(Nội dung bài tập và lời giải chi tiết)
Ví dụ: Bài 1 yêu cầu tính giới hạn của một hàm số. Để giải bài này, chúng ta cần áp dụng các quy tắc tính giới hạn và biến đổi biểu thức để đưa về dạng quen thuộc. Lời giải chi tiết sẽ bao gồm các bước biến đổi và kết luận cuối cùng.
Bài 2 (Trang 20)
(Nội dung bài tập và lời giải chi tiết)
Bài 3 (Trang 21)
(Nội dung bài tập và lời giải chi tiết)
Bài 4 (Trang 22)
(Nội dung bài tập và lời giải chi tiết)
Mẹo giải bài tập Toán 11 hiệu quả
Để giải bài tập Toán 11 một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
- Đọc kỹ đề bài và xác định yêu cầu của bài toán.
- Phân tích các dữ kiện đã cho và tìm mối liên hệ giữa chúng.
- Áp dụng các kiến thức, định lý, tính chất đã học để giải bài toán.
- Kiểm tra lại kết quả và đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập và rèn luyện môn Toán. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Bài tập | Trang | Link giải |
|---|---|---|
| Bài 1 | 19 | Giải bài 1 |
| Bài 2 | 20 | Giải bài 2 |