Giải mục 1 trang 25 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 25 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn! Chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho bài tập mục 1 trang 25 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, tusach.vn luôn cố gắng cung cấp những giải pháp học tập hiệu quả nhất, giúp bạn đạt kết quả tốt nhất.
Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác.
Hoạt động 1
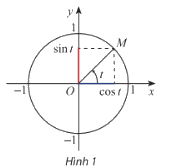
Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác. Sử dụng định nghĩa của các giá trị lượng giác, hãy giải thích vì sao xác định duy nhất:
a) Giá trị sint và cost
b) Giá trị tant (nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)) và \(\cot t\)(nếu \(t \ne k\pi ,k \in \mathbb{Z}\)).
Phương pháp giải:
Quan sát hình vẽ để trả lời.
Lời giải chi tiết:
a) Ta thấy \(\sin t = {y_M}\) là tung độ của điểm M trên đường tròn lượng giác và c\(\cos t = {x_M}\)là hoành độ của điểm M trên đường tròn lượng giác.
Với mỗi điểm M xác định, ta chỉ có 1 tung độ và hoành độ duy nhất
Nên ta chỉ xác định duy nhất giá trị sint và cost.
b,
Nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\), ta có: \(\tan t = \frac{{\sin t}}{{{\rm{cost}}}} = \frac{{{y_M}}}{{{x_M}}}\)( \({x_M} \ne 0\))
Nếu \(t \ne k\pi ,k \in \mathbb{Z}\), ta có: \(\cot t = \frac{{{\rm{cost}}}}{{{\rm{sint}}}} = \frac{{{x_M}}}{{{y_M}}}\)( \({y_M} \ne 0\))
Do \({x_M}\), \({y_M}\)xác định duy nhất nên \(\tan t\), \(\cot t\)xác định duy nhất.
Giải mục 1 trang 25 SGK Toán 11 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 1 trang 25 SGK Toán 11 tập 1 Chân trời sáng tạo thường xoay quanh các khái niệm cơ bản về hàm số, bao gồm tập xác định, tập giá trị, và cách xác định hàm số bằng đồ thị. Việc nắm vững những kiến thức này là nền tảng quan trọng để học tốt các phần tiếp theo của chương trình.
Nội dung chính của Mục 1 trang 25
- Khái niệm hàm số: Định nghĩa hàm số, các yếu tố của hàm số (biến độc lập, biến phụ thuộc).
- Tập xác định của hàm số: Điều kiện để hàm số có nghĩa, cách tìm tập xác định.
- Tập giá trị của hàm số: Phạm vi các giá trị mà hàm số có thể nhận được.
- Cách xác định hàm số bằng đồ thị: Phân tích đồ thị để xác định hàm số, các tính chất của hàm số.
Bài tập thường gặp trong Mục 1 trang 25
Các bài tập trong mục này thường yêu cầu học sinh:
- Xác định tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Xác định hàm số từ đồ thị.
- Vẽ đồ thị của hàm số.
- Giải các bài toán ứng dụng liên quan đến hàm số.
Lời giải chi tiết cho từng bài tập
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 25 SGK Toán 11 tập 1 Chân trời sáng tạo:
Bài 1: (Ví dụ minh họa)
Cho hàm số y = f(x) = √(x - 2). Hãy xác định tập xác định của hàm số.
Lời giải:
Hàm số y = f(x) = √(x - 2) xác định khi và chỉ khi x - 2 ≥ 0, tức là x ≥ 2. Vậy tập xác định của hàm số là D = [2, +∞).
Bài 2: (Ví dụ minh họa)
Cho hàm số y = g(x) = 1/(x + 1). Hãy xác định tập giá trị của hàm số.
Lời giải:
Hàm số y = g(x) = 1/(x + 1) xác định khi x ≠ -1. Vì x có thể nhận bất kỳ giá trị nào khác -1, nên y có thể nhận bất kỳ giá trị nào khác 0. Vậy tập giá trị của hàm số là R \ {0}.
Mẹo học tập hiệu quả
- Nắm vững định nghĩa: Hiểu rõ các khái niệm cơ bản về hàm số là chìa khóa để giải quyết các bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng đồ thị: Đồ thị là công cụ hữu ích để hình dung và hiểu rõ hơn về hàm số.
- Tham khảo tài liệu: Sử dụng SGK, sách bài tập, và các nguồn tài liệu trực tuyến để bổ sung kiến thức.
Tại sao nên chọn tusach.vn?
tusach.vn cam kết cung cấp:
- Lời giải chi tiết, chính xác và dễ hiểu.
- Đội ngũ giáo viên giàu kinh nghiệm.
- Cập nhật liên tục các bài giải mới nhất.
- Giao diện thân thiện, dễ sử dụng.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | Xem chi tiết tại đây |
| Bài 2 | Xem chi tiết tại đây |