Lý thuyết Phép tính lôgarit - Toán 11 Chân trời sáng tạo
Tổng quan nội dung
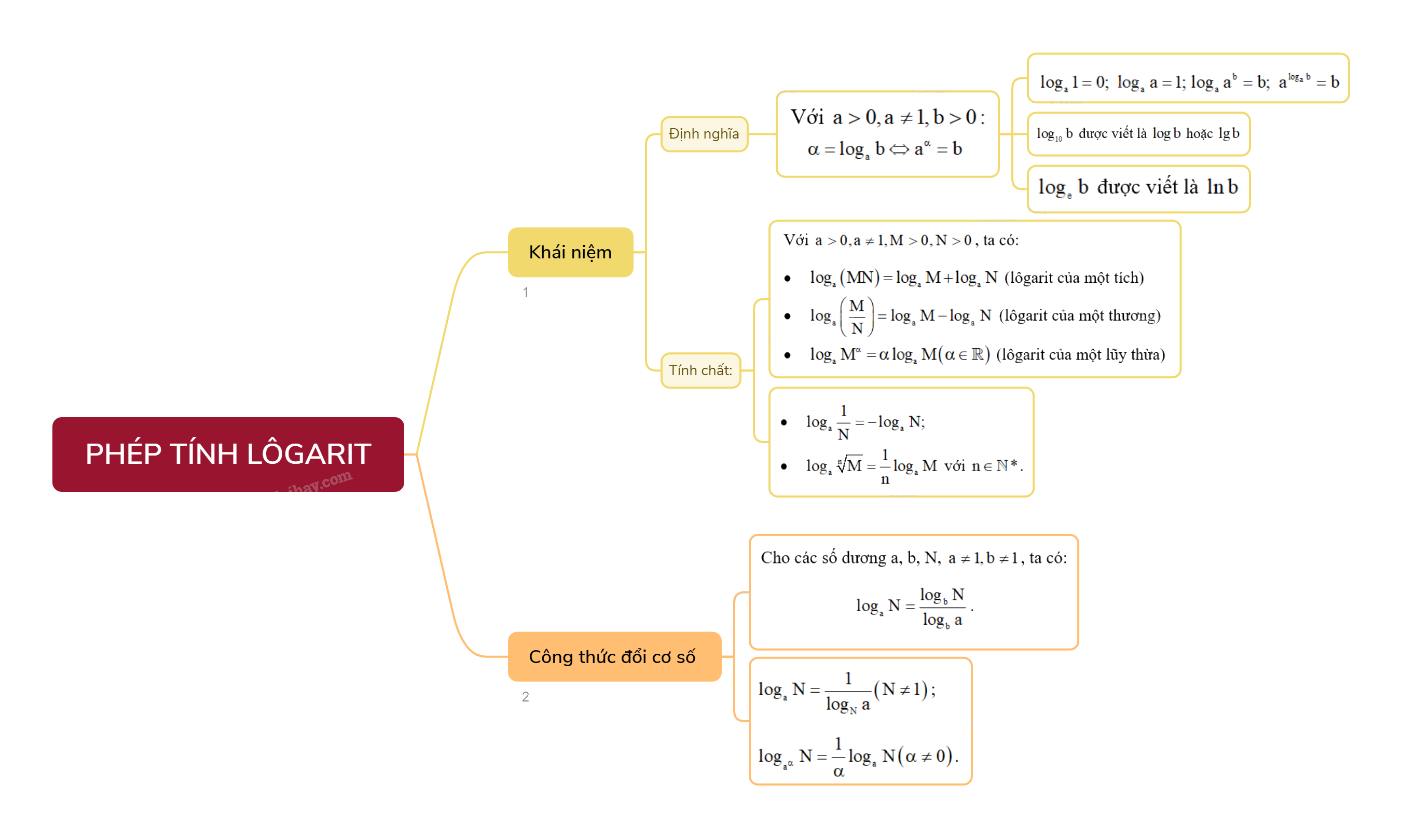
Lý Thuyết Phép Tính Lôgarit - Toán 11 Chân Trời Sáng Tạo
Chào mừng bạn đến với bài học lý thuyết về phép tính lôgarit trong chương trình Toán 11 Chân trời sáng tạo. Đây là một phần kiến thức quan trọng, nền tảng cho nhiều bài toán và ứng dụng trong toán học và các lĩnh vực khác.
Bài viết này sẽ cung cấp một cách đầy đủ và dễ hiểu nhất về định nghĩa, tính chất, các dạng bài tập thường gặp và cách giải chúng.
1. Khái niệm lôgarit Cho hai số thực dương a, b với \(a \ne 1\). Số thực \(\alpha \) thỏa mãn đẳng thức \({a^\alpha } = b\) được gọi là lôgarit cơ số a của b và kí hiệu là \({\log _a}b\).
1. Khái niệm lôgarit
Cho hai số thực dương a, b với \(a \ne 1\). Số thực \(\alpha \) thỏa mãn đẳng thức \({a^\alpha } = b\) được gọi là lôgarit cơ số a của b và kí hiệu là \({\log _a}b\).
\(\alpha = {\log _a}b \Leftrightarrow {a^\alpha } = b\).
Chú ý:
Từ định nghĩa, ta có:
- \({\log _a}1 = 0;\,\,\,{\log _a}a = 1;\,\,{\log _a}{a^b} = b;\,\,\,{a^{{{\log }_a}b}} = b\).
- \({\log _{10}}b\) được viết là \(\log b\) hoặc \(\lg b\);
- \({\log _e}b\) được viết là \(\ln b\).
2. Tính chất
Với \(a > 0,a \ne 1,M > 0,N > 0\), ta có:
- \({\log _a}\left( {MN} \right) = {\log _a}M + {\log _a}N\) (lôgarit của một tích)
- \({\log _a}\left( {\frac{M}{N}} \right) = {\log _a}M - {\log _a}N\) (lôgarit của một thương)
- \({\log _a}{M^\alpha } = \alpha {\log _a}M\,\left( {\alpha \in \mathbb{R}} \right)\) (lôgarit của một lũy thừa)
Chú ý: Đặc biệt, ta có:
- \({\log _a}\frac{1}{N} = - {\log _a}N;\)
- \({\log _a}\sqrt[n]{M} = \frac{1}{n}{\log _a}M\) với \(n \in \mathbb{N}*\).
3. Công thức đổi cơ số
Cho các số dương a, b, N, \(a \ne 1,b \ne 1\), ta có:
\({\log _a}N = \frac{{{{\log }_b}N}}{{{{\log }_b}a}}\).
Đặc biệt, ta có:
\({\log _a}N = \frac{1}{{{{\log }_N}a}}\left( {N \ne 1} \right)\); \({\log _{{a^\alpha }}}N = \frac{1}{\alpha }{\log _a}N\left( {\alpha \ne 0} \right)\).
Lý Thuyết Phép Tính Lôgarit - Toán 11 Chân Trời Sáng Tạo: Tổng Quan
Phép tính lôgarit là một trong những khái niệm quan trọng trong toán học, đặc biệt là trong chương trình Toán 11. Nó đóng vai trò then chốt trong việc giải quyết các bài toán mũ và các bài toán liên quan đến tăng trưởng, suy giảm. Bài viết này sẽ đi sâu vào lý thuyết phép tính lôgarit theo chương trình Chân trời sáng tạo, cung cấp kiến thức nền tảng vững chắc cho học sinh.
1. Định Nghĩa Lôgarit
Lôgarit của một số dương b theo cơ số a (với a > 0 và a ≠ 1) là số x sao cho ax = b. Ký hiệu: x = logab.
- a: Cơ số của lôgarit.
- b: Số bị lôgarit (luôn dương).
- x: Lôgarit của b theo cơ số a.
2. Các Tính Chất Quan Trọng của Lôgarit
Việc nắm vững các tính chất của lôgarit là rất quan trọng để đơn giản hóa các biểu thức và giải các bài toán liên quan. Dưới đây là một số tính chất cơ bản:
- Lôgarit của tích:loga(xy) = logax + logay
- Lôgarit của thương:loga(x/y) = logax - logay
- Lôgarit của lũy thừa:loga(xn) = n logax
- Đổi cơ số lôgarit:logab = logcb / logca
- Lôgarit cơ số 10 (Lôgarit thập phân):log10x thường được ký hiệu là lg x
- Lôgarit cơ số e (Lôgarit tự nhiên):logex thường được ký hiệu là ln x
3. Các Dạng Bài Tập Thường Gặp và Cách Giải
Dưới đây là một số dạng bài tập thường gặp về phép tính lôgarit và hướng dẫn giải:
3.1. Tính Giá Trị Biểu Thức Lôgarit
Sử dụng các tính chất của lôgarit để biến đổi biểu thức về dạng đơn giản nhất và tính giá trị.
Ví dụ: Tính giá trị của biểu thức log28 + log24
Giải:log28 + log24 = log2(8*4) = log232 = 5
3.2. Giải Phương Trình Lôgarit
Sử dụng các tính chất của lôgarit để đưa phương trình về dạng cơ bản và giải.
Ví dụ: Giải phương trình log3(x+2) = 2
Giải:x+2 = 32 = 9 => x = 7
3.3. So Sánh Các Lôgarit
Sử dụng hàm số lôgarit và các tính chất của hàm số để so sánh các lôgarit.
4. Ứng Dụng của Phép Tính Lôgarit
Phép tính lôgarit có nhiều ứng dụng trong thực tế, bao gồm:
- Tính độ lớn của động đất (Richter scale): Độ lớn của động đất được tính bằng công thức logarit.
- Tính độ pH của dung dịch: Độ pH được tính bằng công thức logarit.
- Tính lãi kép: Công thức tính lãi kép sử dụng hàm mũ và logarit.
- Trong khoa học máy tính: Phép tính logarit được sử dụng trong các thuật toán và cấu trúc dữ liệu.
5. Bài Tập Vận Dụng
Để củng cố kiến thức, bạn hãy thử giải các bài tập sau:
- Tính giá trị của biểu thức: log525 - log55
- Giải phương trình: log2(2x-1) = 3
- So sánh: log23 và log32
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và đầy đủ về lý thuyết phép tính lôgarit trong chương trình Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!