Giải mục 2 trang 66, 67 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 66, 67 SGK Toán 11 tập 2 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 66, 67 SGK Toán 11 tập 2, chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Bài tập này thuộc chương trình học Toán 11, tập trung vào các kiến thức về...
Từ một điểm (O) vẽ hai tia (Ox) và (Oy) lần lượt vuông góc với hai bức tường trong phòng. Đo góc (xOy).
Hoạt động 2
Từ một điểm \(O\) vẽ hai tia \(Ox\) và \(Oy\) lần lượt vuông góc với hai bức tường trong phòng. Đo góc \(xOy\).
Phương pháp giải:
Thực hành đo góc và trả lời câu hỏi.
Lời giải chi tiết:
\(\widehat {xOy} = {90^ \circ }\).
Hoạt động 3
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\) điểm \(M\) không thuộc \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(H\) và \(K\) lần lượt là hình chiếu vuông góc của \(M\) lên \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(O\) là giao điểm của \(d\) và \(\left( {MHK} \right)\) (Hình 8).

a) Giả sử \(\left( P \right) \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tìm trong \(\left( P \right)\) đường thẳng vuông góc với \(\left( Q \right)\).
b) Giả sử \(\left( P \right)\) chứa đường thẳng \(a\) với \(a \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tính góc giữa \(\left( P \right)\) và \(\left( Q \right)\).
Phương pháp giải:
Sử dụng định nghĩa: Góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) là góc giữa hai đường thẳng lần lượt vuông góc với \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot OH\\MK \bot \left( Q \right) \Rightarrow MK \bot OK\\\left( {\left( P \right),\left( Q \right)} \right) = {90^ \circ } \Rightarrow \left( {MH,MK} \right) = {90^ \circ } \Rightarrow MH \bot MK\end{array}\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HMK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
Trong \(\left( P \right)\) có đường thẳng \(OH\) vuông góc với \(\left( Q \right)\).
b) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right) \Rightarrow a \bot OK\\MH \bot \left( P \right) \Rightarrow MH \bot a\end{array} \right\} \Rightarrow MH\parallel OK\)
Lại có \(MH \bot \left( P \right)\). Vậy \(OK \bot \left( P \right) \Rightarrow OK \bot OH\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HOK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
\(\left( {\left( P \right),\left( Q \right)} \right) = \left( {MH,MK} \right) = \widehat {HMK} = {90^ \circ }\).
Thực hành 1
Cho hình chóp \(S.ABCD\) có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng:
a) \(\left( {SAC} \right) \bot \left( {ABCD} \right)\);
b) \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Phương pháp giải:
Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.
Lời giải chi tiết:

a) Gọi \(O = AC \cap B{\rm{D}}\).
Tam giác \(SAC\) cân tại \(S \Rightarrow SO \bot AC\)
Tam giác \(SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow SO \bot \left( {ABCD} \right)\\SO \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow \left( {SAC} \right) \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(SO \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\\AC \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow \left( {SAC} \right) \bot \left( {SB{\rm{D}}} \right)\)
Vận dụng 1
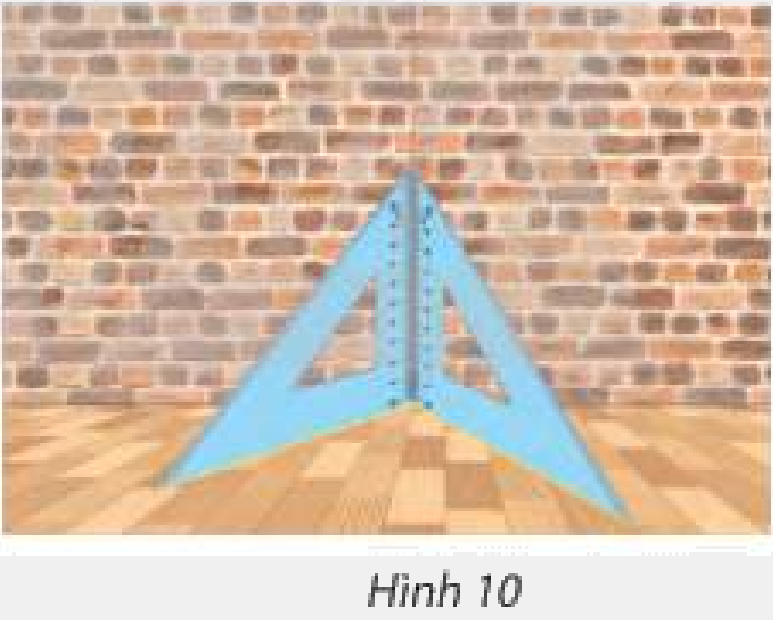
Mô tả cách kiểm tra một bức tường vuông góc với mặt sàn bằng hai cái êke trong Hình 10.

Phương pháp giải:
Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
Đặt êke sao cho hai cạnh góc vuông của hai êke chạm nhau tạo thành một đường thẳng, hai cạnh còn lại của hai êke sát với mặt sàn.
Nếu đường thẳng đó nằm sát với bức tường thì bức tường vuông góc với mặt sàn.
Giải mục 2 trang 66, 67 SGK Toán 11 tập 2 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 2 trang 66, 67 SGK Toán 11 tập 2 Chân trời sáng tạo là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về... (nêu rõ kiến thức trọng tâm của mục này). Tusach.vn xin giới thiệu lời giải chi tiết cho từng bài tập, giúp các em hiểu rõ bản chất và phương pháp giải.
Bài 1: (Nêu lại đề bài Bài 1)
Lời giải:
...
Bài 2: (Nêu lại đề bài Bài 2)
Lời giải:
...
Bài 3: (Nêu lại đề bài Bài 3)
Lời giải:
...
Các kiến thức liên quan cần nắm vững
- Khái niệm về...: Giải thích rõ ràng khái niệm.
- Công thức...: Liệt kê và giải thích các công thức quan trọng.
- Phương pháp giải...: Hướng dẫn các bước giải bài tập liên quan.
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong mục 2 trang 66, 67 SGK Toán 11 tập 2 một cách nhanh chóng và hiệu quả, các em có thể áp dụng một số mẹo sau:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Phân tích các dữ kiện đã cho và tìm mối liên hệ giữa chúng.
- Sử dụng các công thức và định lý phù hợp.
- Kiểm tra lại kết quả sau khi giải xong.
Ví dụ minh họa
Ví dụ: (Đưa ra một ví dụ cụ thể và giải chi tiết)
Luyện tập thêm
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập sau:
- Bài tập tương tự trong SGK và sách bài tập.
- Các bài tập trực tuyến trên các trang web học tập.
Tổng kết
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 66, 67 SGK Toán 11 tập 2 Chân trời sáng tạo. Tusach.vn luôn sẵn sàng hỗ trợ các em trong quá trình học tập. Chúc các em học tốt!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Link đến lời giải chi tiết bài 1) |
| Bài 2 | (Link đến lời giải chi tiết bài 2) |
| Bài 3 | (Link đến lời giải chi tiết bài 3) |