Bài 10 trang 87 Toán 11 Tập 2 - Chân trời sáng tạo

Bài 10 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo

Bài 10 trang 87 SGK Toán 11 Tập 2 – Chân trời sáng tạo

Bài 10 trang 87 SGK Toán 11 Tập 2 thuộc chương trình Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Cấp số cho và cấp số nhân. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán thực tế liên quan đến cấp số.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = a\).

Đề bài

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = a\). Gọi \(M,N,P\) lần lượt là trung điểm của \(SB,SC\) và \(SD\). Tính khoảng cách giữa \(AM\) và \(NP\).

Phương pháp giải - Xem chi tiết Bài 10 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo 1

Cách tính khoảng cách giữa hai đường thẳng chéo nhau:

Cách 1: Dựng đường vuông góc chung.

Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.

Lời giải chi tiết

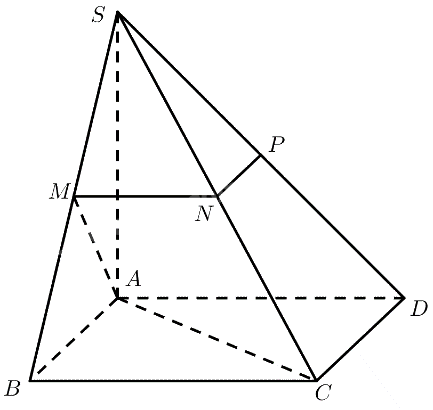
Bài 10 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo 2

\(M\) là trung điểm của \(SB\)

\(N\) là trung điểm của \(SC\)

\( \Rightarrow MN\) là đường trung bình của \(\Delta SBC\)

\(\left. \begin{array}{l} \Rightarrow MN\parallel BC\\BC \bot C{\rm{D}}\end{array} \right\} \Rightarrow MN \bot C{\rm{D}}\)

Mà \(C{\rm{D}}\parallel NP\) \( \Rightarrow MN \bot NP\) (1)

\(\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC\\AB \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right)\)

Mà \(MN\parallel BC\)\( \Rightarrow MN \bot \left( {SAB} \right) \Rightarrow MN \bot AM\)(2)

Từ (1) và (2) \( \Rightarrow d\left( {AM,NP} \right) = MN = \frac{1}{2}BC = \frac{a}{2}\).

Bài 10 trang 87 SGK Toán 11 Tập 2 – Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 10 trang 87 SGK Toán 11 Tập 2 Chân trời sáng tạo là một bài tập quan trọng trong chương trình ôn tập về cấp số cho và cấp số nhân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức và phương pháp giải liên quan đến hai loại cấp số này.

Nội dung bài tập

Bài tập yêu cầu học sinh giải các bài toán liên quan đến:

Xác định cấp số cho và cấp số nhân.
Tính số hạng tổng quát của cấp số.
Tính tổng của n số hạng đầu tiên của cấp số.
Ứng dụng cấp số vào giải quyết các bài toán thực tế.

Lời giải chi tiết

Dưới đây là lời giải chi tiết cho từng phần của bài tập:

Phần 1: Xác định cấp số

Để xác định một dãy số là cấp số cho hay cấp số nhân, ta cần kiểm tra hiệu hoặc thương của hai số hạng liên tiếp có là một hằng số hay không. Nếu hiệu là hằng số, dãy số đó là cấp số cho. Nếu thương là hằng số, dãy số đó là cấp số nhân.

Phần 2: Tính số hạng tổng quát

Số hạng tổng quát của cấp số cho được tính theo công thức: u_n = u₁ + (n - 1)d, trong đó u₁ là số hạng đầu tiên, d là công sai và n là số thứ tự của số hạng.

Số hạng tổng quát của cấp số nhân được tính theo công thức: u_n = u₁ * q^{(n - 1)}, trong đó u₁ là số hạng đầu tiên, q là công bội và n là số thứ tự của số hạng.

Phần 3: Tính tổng của n số hạng đầu tiên

Tổng của n số hạng đầu tiên của cấp số cho được tính theo công thức: S_n = (n/2) * (u₁ + u_n) hoặc S_n = (n/2) * [2u₁ + (n - 1)d].

Tổng của n số hạng đầu tiên của cấp số nhân được tính theo công thức: S_n = u₁ * (1 - qⁿ) / (1 - q) (với q ≠ 1).

Ví dụ minh họa

Ví dụ: Cho cấp số cho có số hạng đầu tiên u₁ = 2 và công sai d = 3. Tính số hạng thứ 5 và tổng của 5 số hạng đầu tiên.

Giải:

Số hạng thứ 5: u₅ = u₁ + (5 - 1)d = 2 + 4 * 3 = 14
Tổng của 5 số hạng đầu tiên: S₅ = (5/2) * (u₁ + u₅) = (5/2) * (2 + 14) = 40

Lưu ý khi giải bài tập

Đọc kỹ đề bài để xác định đúng loại cấp số và các thông tin cần thiết.
Sử dụng đúng công thức để tính toán.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Tài liệu tham khảo

Ngoài SGK Toán 11 Tập 2 Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 11
Các trang web học toán trực tuyến
Các video hướng dẫn giải bài tập Toán 11

tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh sẽ tự tin hơn khi giải Bài 10 trang 87 SGK Toán 11 Tập 2 Chân trời sáng tạo. Chúc các bạn học tốt!