Bài 7 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 7 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài 7 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo là bài tập thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
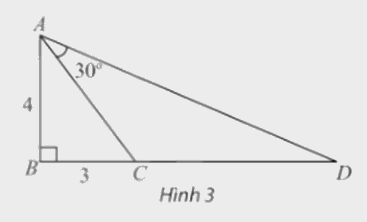
Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3.
Đề bài
Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn \(\widehat {CAD} = {30^0}\). Tính \(\tan \widehat {BAD}\), từ đó tính độ dài cạnh CD.
Phương pháp giải - Xem chi tiết
Nhìn hình vẽ để tính \(\tan \widehat {BAC}\), sau đó áp dụng công thức cộng để tính \(\tan \widehat {BAD}\).
Lời giải chi tiết
Xét tam giác ABC vuông tại B có:
\(\tan \widehat {BAC} = \frac{3}{4}\)
Suy ra, \(\tan \widehat {BAD} = \tan \left( {\widehat {BAC} + \widehat {CAD}} \right) = \tan \left( {\widehat {BAC} + {{30}^0}} \right)\)
\( = \frac{{\tan \widehat {BAC} + \tan {{30}^0}}}{{1 - \tan \widehat {BAC}.\tan {{30}^0}}} = \frac{{\frac{3}{4} + \frac{{\sqrt 3 }}{3}}}{{1 - \frac{3}{4}.\frac{{\sqrt 3 }}{3}}} \approx 2,34\)
Xét tam giác vuông ABD vuông tại B có:
\(\begin{array}{l}BD = AB.\tan \widehat {BAD} = 4.2,34 \approx 9,36\\ \Rightarrow CD = BD - BC \approx 9,36 - 3 \approx 6,36\end{array}\)
Bài 7 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 7 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về giới hạn của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài tập yêu cầu tính giới hạn của hàm số tại một điểm cho trước. Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của giới hạn hàm số, cũng như các phương pháp tính giới hạn thường gặp.
Lời giải chi tiết
Để giải bài tập này, ta có thể sử dụng các phương pháp sau:
- Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào hàm số để tính giới hạn.
- Phương pháp phân tích thành nhân tử: Phân tích tử số và mẫu số thành nhân tử để rút gọn biểu thức và tính giới hạn.
- Phương pháp nhân liên hợp: Nhân tử số và mẫu số với liên hợp của biểu thức để khử dạng vô định.
- Sử dụng định lý giới hạn: Áp dụng các định lý giới hạn để tính giới hạn của hàm số.
Ví dụ, giả sử bài tập yêu cầu tính limx→2 (x2 - 4) / (x - 2). Ta có thể phân tích tử số thành nhân tử như sau:
(x2 - 4) = (x - 2)(x + 2)
Khi đó, biểu thức trở thành:
limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 4
Các dạng bài tập tương tự
Ngoài bài tập này, còn rất nhiều bài tập tương tự về giới hạn hàm số. Để rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo các bài tập sau:
- Tính giới hạn của hàm số tại một điểm cho trước.
- Tìm giới hạn của hàm số khi x tiến tới vô cùng.
- Chứng minh sự tồn tại của giới hạn hàm số.
Mẹo giải bài tập
Để giải bài tập về giới hạn hàm số một cách hiệu quả, học sinh nên:
- Nắm vững các định nghĩa và tính chất của giới hạn hàm số.
- Luyện tập thường xuyên để làm quen với các phương pháp tính giới hạn.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
- Tham khảo các tài liệu tham khảo và lời giải chi tiết.
Tầm quan trọng của bài tập
Bài tập về giới hạn hàm số là một phần quan trọng trong chương trình học Toán 11. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp học sinh:
- Hiểu rõ khái niệm giới hạn hàm số.
- Vận dụng kiến thức vào giải quyết các bài toán thực tế.
- Chuẩn bị tốt cho các kỳ thi quan trọng.
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh sẽ tự tin hơn trong việc giải Bài 7 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo và các bài tập tương tự. Chúc các bạn học tốt!
| STT | Bài tập | Lời giải |
|---|---|---|
| 1 | Bài 7a | Xem tại đây |
| 2 | Bài 7b | Xem tại đây |