Giải mục 3 trang 67, 68, 69 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 67, 68, 69 SGK Toán 11 tập 2 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 67, 68, 69 SGK Toán 11 tập 2, chương trình Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải các bài tập một cách dễ hiểu nhất.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, tusach.vn luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ các em học tập hiệu quả.
Cho đường thẳng (a) vuông góc với mặt phẳng (left( Q right)).
Hoạt động 4
Cho đường thẳng \(a\) vuông góc với mặt phẳng \(\left( Q \right)\). Mặt phẳng \(\left( P \right)\) chứa \(a\) và cắt \(\left( Q \right)\) theo giao tuyến \(c\). Trong \(\left( Q \right)\) ta vẽ đường thẳng \(b\) vuông góc với \(c\).
Hỏi:
a) \(\left( P \right)\) có vuông góc với \(\left( Q \right)\) không?
b) Đường thẳng \(b\) vuông góc với \(\left( P \right)\) không?
Phương pháp giải:
Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \left( P \right) \bot \left( Q \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}a \bot \left( Q \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow a \bot b\\b \bot c\\a,c \subset \left( P \right)\end{array} \right\} \Rightarrow b \bot \left( P \right)\)
Hoạt động 5
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Gọi \(a\) là giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\). Lấy điểm \(M\) trong \(\left( R \right)\), vẽ hai đường thẳng \(MH\) và \(MK\) lần lượt vuông góc với \(\left( P \right)\) và \(\left( Q \right)\). Hỏi:

a) Hai đường thẳng \(MH\) và \(MK\) có nằm trong \(\left( R \right)\) không?
b) Đường thẳng \(a\) có vuông góc với \(\left( R \right)\) không?
Phương pháp giải:
Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( R \right)\\MH \bot \left( P \right)\\\left( R \right) \bot \left( P \right)\end{array} \right\} \Rightarrow MH \subset \left( R \right)\\\left. \begin{array}{l}M \in \left( R \right)\\MK \bot \left( Q \right)\\\left( R \right) \bot \left( Q \right)\end{array} \right\} \Rightarrow MK \subset \left( R \right)\end{array}\)
b) Ta có:
\(\left. \begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot a\\MK \bot \left( Q \right) \Rightarrow MK \bot a\\MH,MK \subset \left( R \right)\end{array} \right\} \Rightarrow a \bot \left( R \right)\)
Thực hành 2
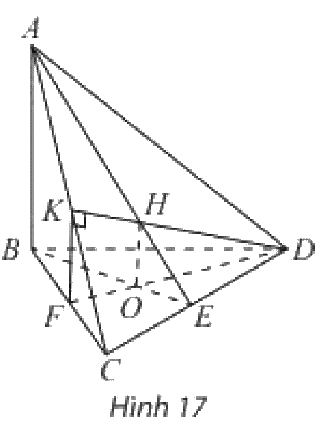
Tứ diện \(ABCD\) có \(AB \bot \left( {BCD} \right)\). Trong tam giác \(BCD\) vẽ đường cao \(BE\) và \(DF\) cắt nhau tại \(O\). Trong mặt phẳng \(\left( {ACD} \right)\) vẽ \({\rm{D}}K\) vuông góc với \(AC\) tại \(K\). Gọi \(H\) là trực tâm của tam giác \(ACD\). Chứng minh rằng:

a) \(\left( {ADC} \right) \bot \left( {ABE} \right)\) và \(\left( {ADC} \right) \bot \left( {DFK} \right)\);
b) \(OH \bot \left( {ADC} \right)\).
Phương pháp giải:
‒ Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng:
+ Cách 1: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
+ Cách 2: sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)\)
Lại có \(C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {ABE} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}\)
Lại có \(AC \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {DFK} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)\)
Vận dụng 2
Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn.
Phương pháp giải:
Sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
Lời giải chi tiết:
Ta mở quyển sách ra và đặt quyển sách lên mặt bàn sao cho hai mép dưới của bìa sách nằm trên mặt bàn.
Giải mục 3 trang 67, 68, 69 SGK Toán 11 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 3 trong SGK Toán 11 tập 2, chương trình Chân trời sáng tạo, tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Đây là một phần quan trọng, đặt nền móng cho các kiến thức hình học không gian phức tạp hơn ở các lớp trên. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Nội dung chính của Mục 3
- Vị trí tương đối của hai đường thẳng trong không gian: Song song, cắt nhau, chéo nhau.
- Góc giữa hai đường thẳng trong không gian: Định nghĩa, cách tính góc.
- Vị trí tương đối của đường thẳng và mặt phẳng trong không gian: Nằm trong mặt phẳng, song song với mặt phẳng, cắt mặt phẳng.
- Góc giữa đường thẳng và mặt phẳng trong không gian: Định nghĩa, cách tính góc.
Giải chi tiết các bài tập trang 67, 68, 69
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 3, trang 67, 68, 69 SGK Toán 11 tập 2 - Chân trời sáng tạo:
Bài 1: (Trang 67)
(Đề bài)
Lời giải:
(Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết)
Bài 2: (Trang 68)
(Đề bài)
Lời giải:
(Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết)
Bài 3: (Trang 69)
(Đề bài)
Lời giải:
(Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết)
Mẹo giải bài tập hiệu quả
- Nắm vững định nghĩa và tính chất: Đây là nền tảng để giải quyết mọi bài toán.
- Vẽ hình minh họa: Hình vẽ giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng các công thức và định lý: Áp dụng đúng công thức và định lý sẽ giúp bạn giải bài tập nhanh chóng và chính xác.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo thêm
Để hiểu sâu hơn về các kiến thức trong mục 3, các em có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11 tập 2 - Chân trời sáng tạo
- Các trang web học toán trực tuyến uy tín
- Video bài giảng của các thầy cô giáo
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải các bài tập Toán 11 tập 2. Chúc các em học tập tốt!