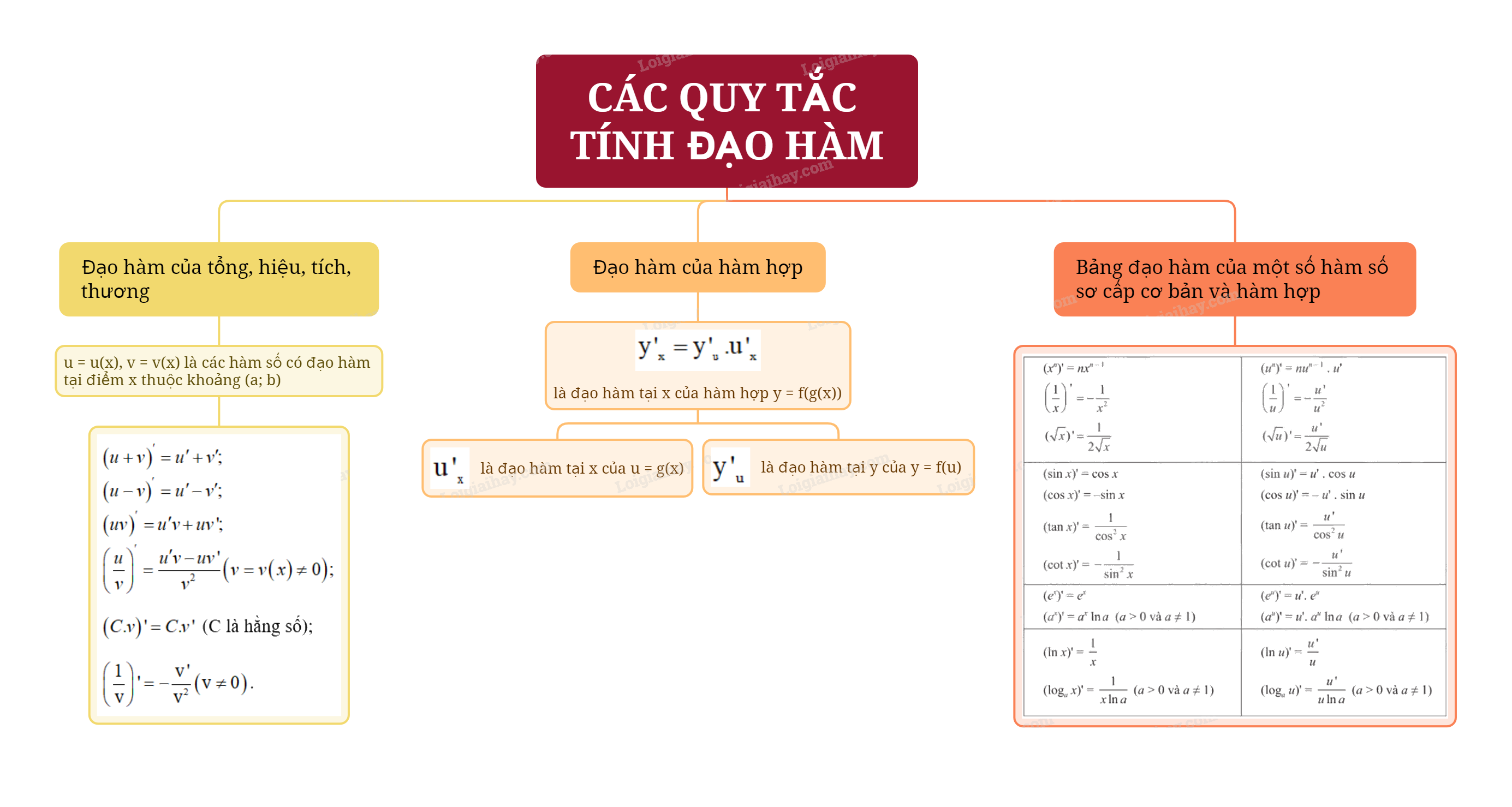
Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Các Quy Tắc Tính Đạo Hàm - Toán 11 Chân Trời Sáng Tạo
Bài viết này cung cấp đầy đủ và chi tiết lý thuyết về các quy tắc tính đạo hàm trong chương trình Toán 11 Chân Trời Sáng Tạo. Chúng tôi sẽ trình bày một cách dễ hiểu, kèm theo ví dụ minh họa để bạn có thể nắm vững kiến thức một cách nhanh chóng.
Nội dung bao gồm các quy tắc đạo hàm cơ bản, quy tắc đạo hàm của hàm hợp, quy tắc đạo hàm của hàm lượng giác, hàm mũ, hàm logarit và các ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
1. Đạo hàm của tổng, hiệu, tích, thương Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc tập xác định.
1. Đạo hàm của tổng, hiệu, tích, thương
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc tập xác định. Khi đó
\(\begin{array}{*{20}{l}}{{{\left( {u + v} \right)}^\prime } = u' + v';}\\{{{\left( {u - v} \right)}^\prime } = u' - v';}\\{{{\left( {uv} \right)}^\prime } = u'v + uv';}\\{{{\left( {\frac{u}{v}} \right)}^\prime } = \frac{{u'v - uv'}}{{{v^2}}}\left( {v = v\left( x \right) \ne 0} \right);}\end{array}\)
\(\left( {C.v} \right)' = C.v'\) (C là hằng số);
\(\left( {\frac{1}{v}} \right)' = - \frac{{v'}}{{{v^2}}}\left( {v \ne 0} \right)\).
2. Đạo hàm của hàm hợp
Nếu hàm số u = g(x) có đạo hàm tại x là \(u{'_x}\) và hàm số y = f(u) có đạo hàm tại y là \(y{'_u}\) thì hàm hợp y = f(g(x)) có đạo hàm tại x là \(y{'_x} = y{'_u}.u{'_x}\).
3. Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp
4. Đạo hàm cấp hai
Cho hàm số y = f(x) có đạo hàm tại mọi điểm \(x \in \left( {a;b} \right)\) thì ta có hàm số \(y' = f'\left( x \right)\) xác định trên (a; b).
Nếu hàm số y’ = f’(x) lại có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) tại x, kí hiệu là y” hoặc f”(x).
\(f''\left( x \right) = \left( {f'\left( x \right)} \right)'\).
Ý nghĩa cơ học của đạo hàm cấp hai
Đạo hàm cấp hai f”(t) là gia tốc tức thời tại thời điểm t của vân chuyển động có phương trình \(s = f\left( t \right)\).
Lý Thuyết Các Quy Tắc Tính Đạo Hàm - Toán 11 Chân Trời Sáng Tạo: Tổng Quan
Đạo hàm là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc nghiên cứu sự thay đổi của hàm số. Trong chương trình Toán 11 Chân Trời Sáng Tạo, học sinh sẽ được làm quen với các quy tắc tính đạo hàm cơ bản, giúp đơn giản hóa quá trình tìm đạo hàm của các hàm số phức tạp.
1. Các Quy Tắc Đạo Hàm Cơ Bản
Dưới đây là các quy tắc đạo hàm cơ bản mà bạn cần nắm vững:
- Quy tắc đạo hàm của hằng số: (c)' = 0, với c là hằng số.
- Quy tắc đạo hàm của hàm số mũ: (xn)' = nxn-1, với n là số thực.
- Quy tắc đạo hàm của hàm số lượng giác:
- (sin x)' = cos x
- (cos x)' = -sin x
- (tan x)' = 1/cos2 x
- (cot x)' = -1/sin2 x
- Quy tắc đạo hàm của hàm số logarit: (loga x)' = 1/(x ln a)
- Quy tắc đạo hàm của hàm số mũ: (ax)' = ax ln a
2. Quy Tắc Đạo Hàm của Hàm Hợp
Nếu y = f(u) và u = g(x), thì đạo hàm của y theo x được tính bằng công thức:
(y)' = (f'(u)) * (g'(x))
Ví dụ: Tính đạo hàm của hàm số y = sin(x2). Ở đây, f(u) = sin(u) và g(x) = x2. Vậy (y)' = cos(u) * 2x = cos(x2) * 2x = 2x cos(x2).
3. Quy Tắc Đạo Hàm của Tổng, Hiệu, Tích và Thương
Quy tắc đạo hàm của tổng/hiệu: (u ± v)' = u' ± v'
Quy tắc đạo hàm của tích: (uv)' = u'v + uv'
Quy tắc đạo hàm của thương: (u/v)' = (u'v - uv')/v2
4. Ứng Dụng của Đạo Hàm
Đạo hàm có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác, bao gồm:
- Tìm cực trị của hàm số: Đạo hàm bằng 0 tại các điểm cực trị.
- Nghiên cứu sự biến thiên của hàm số: Dựa vào dấu của đạo hàm để xác định hàm số đồng biến hay nghịch biến.
- Giải các bài toán tối ưu hóa: Tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số trong một khoảng cho trước.
5. Bài Tập Vận Dụng
Để củng cố kiến thức, hãy thử giải các bài tập sau:
- Tính đạo hàm của hàm số f(x) = 3x4 - 2x2 + 5x - 1.
- Tính đạo hàm của hàm số g(x) = cos(2x + 1).
- Tìm đạo hàm của hàm số h(x) = x2 * ex.
6. Lời Khuyên Khi Học Lý Thuyết Đạo Hàm
- Nắm vững các quy tắc đạo hàm cơ bản.
- Luyện tập thường xuyên với nhiều dạng bài tập khác nhau.
- Hiểu rõ ý nghĩa hình học của đạo hàm.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm toán học để kiểm tra kết quả.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết các quy tắc tính đạo hàm trong chương trình Toán 11 Chân Trời Sáng Tạo. Chúc bạn học tập tốt!