Giải mục 3 trang 109, 110 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 109, 110 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài tập mục 3 trang 109, 110 SGK Toán 11 tập 1 Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải bài tập hiệu quả, giúp học sinh hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và dễ hiểu nhất, hỗ trợ tối đa cho quá trình học tập của bạn.
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10).
Hoạt động 3
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
Phương pháp giải:
Để xác định vị trí tương đối của hai đường thẳng, ta dựa vào số điểm chung của hai đường thẳng đó.
Lời giải chi tiết:
Ta có: \(a\parallel \left( P \right) \Rightarrow \) Đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) không có điểm chung.
\(\left( P \right) \cap \left( Q \right) = b \Rightarrow b \subset \left( P \right)\)
Do đó hai đường thẳng \(a,b\) không có điểm chung.
Hoạt động 4
Cho hai đường thẳng chéo nhau \(a,b\). Lấy một điểm \(M\) trên \(a\), vẽ đường thẳng \(b'\) đi qua \(M\) và song song với \(b\). Đặt \(\left( P \right)\) là mặt phẳng đi qua \(a,b'\).
a) Có nhận xét gì về mối liên hệ giữa \(b\) và \(\left( P \right)\).
b) Gọi \(\left( {P'} \right)\) là mặt phẳng chứa \(a\) và song song với \(b\). Có nhận xét gì về mối liên hệ giữa \(b'\) và \(\left( {P'} \right)\); \(\left( P \right)\) và \(\left( {P'} \right)\)?

Phương pháp giải:
Sử dụng hệ quả 1: Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Nếu qua điểm M thuộc \(\left( P \right)\) ta vẽ đường thẳng \(b\) song song với \(a\) thì \(b\) phải nằm trong \(\left( P \right)\).
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}b\parallel b'\\b' \subset \left( P \right)\end{array} \right\} \Rightarrow b\parallel \left( P \right)\)
b) Theo hệ quả 1, ta có:
\(\left. \begin{array}{l}b\parallel \left( {P'} \right)\\M \in b'\\b\parallel b'\end{array} \right\} \Rightarrow b' \subset \left( {P'} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}a \subset \left( P \right)\\a \subset \left( {P'} \right)\end{array} \right\} \Rightarrow a = \left( P \right) \cap \left( {P'} \right)\\\left. \begin{array}{l}b' \subset \left( P \right)\\b' \subset \left( {P'} \right)\end{array} \right\} \Rightarrow b' = \left( P \right) \cap \left( {P'} \right)\end{array}\)
Do đó \(a\) và \(b'\) đều là các đường thẳng chung của hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\).
Vì \(a\) và \(b'\) phân biệt, mà hai mặt phẳng phân biệt chỉ có duy nhất một đường thẳng chung nên \(\left( P \right) \equiv \left( {P'} \right)\).
Thực hành 3
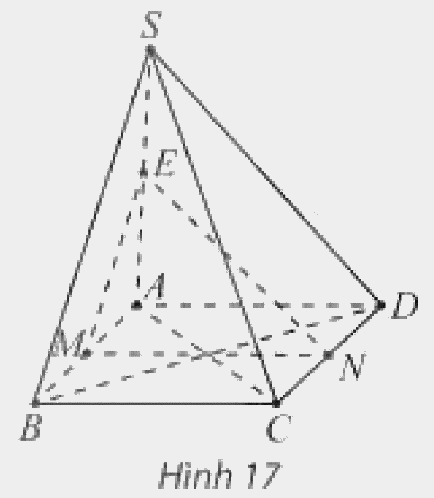
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M,N,E\) lần lượt là trung điểm của các đoạn thẳng \(AB,CD,SA\) (Hình 17). Chứng minh rằng:
a) \(MN\) song song với hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAD} \right)\);
b) \(SB\) và \(SC\) song song với mặt phẳng \(\left( {MNE} \right)\).

Phương pháp giải:
Để chứng minh đường thẳng song song với mặt phẳng, ta chứng minh đường thẳng đấy không nằm trong mặt phẳng và song song với một đường thẳng nằm trong mặt phẳng.
Lời giải chi tiết:
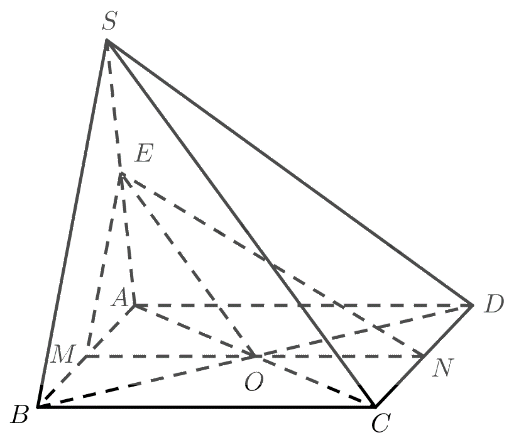
a) \(M\) là trung điểm của \(AB\)
\(N\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABCD\)
\( \Rightarrow MN\parallel A{\rm{D}}\parallel BC\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}MN\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SBC} \right)\\\left. \begin{array}{l}MN\parallel A{\rm{D}}\\A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SA{\rm{D}}} \right)\end{array}\)
b) \(M\) là trung điểm của \(AB\)
\(E\) là trung điểm của \(SA\)
\( \Rightarrow ME\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow ME\parallel SB\\ME \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SB\parallel \left( {MNE} \right)\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
\( \Rightarrow O\) là trung điểm của \(AC\) và \(O,M,N\) thẳng hàng
Mà \(E\) là trung điểm của \(SA\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel SC\\OE \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SC\parallel \left( {MNE} \right)\)
Vận dụng 2
Làm thế nào để đặt cây thước kẻ \(a\) để nó song song các trang của một cuốn sách?
Phương pháp giải:
Sử dụng định lí 1: Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).
Lời giải chi tiết:
Để đặt cây thước kẻ \(a\) song song các trang của một cuốn sách, ta đặt nó song song với mép cuốn sách.
Giải mục 3 trang 109, 110 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Phương pháp giải
Mục 3 trong SGK Toán 11 tập 1 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Trang 109 và 110 thường chứa các bài tập vận dụng kiến thức đã học để giải quyết các vấn đề thực tế. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để hoàn thành tốt các bài tập này.
Nội dung chính của Mục 3
Để hiểu rõ hơn về Mục 3, chúng ta cần xác định nội dung chính mà nó đề cập đến. Thông thường, đây có thể là:
- Các khái niệm mới: Định nghĩa, tính chất, định lý liên quan đến chủ đề.
- Các dạng bài tập: Bài tập áp dụng công thức, bài tập chứng minh, bài tập tìm hiểu thực tế.
- Mục tiêu học tập: Những gì học sinh cần đạt được sau khi học xong Mục 3.
Phương pháp giải bài tập hiệu quả
Để giải quyết các bài tập trong Mục 3 trang 109, 110 SGK Toán 11 tập 1 Chân trời sáng tạo, bạn có thể áp dụng các phương pháp sau:
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và những gì cần tìm.
- Phân tích đề bài: Xác định mối liên hệ giữa các dữ kiện, tìm ra công thức hoặc định lý phù hợp để áp dụng.
- Lập kế hoạch giải: Xác định các bước cần thực hiện để giải quyết bài toán.
- Thực hiện giải: Thực hiện các bước đã lập, kiểm tra lại kết quả.
- Kiểm tra lại kết quả: Đảm bảo kết quả thu được phù hợp với yêu cầu của đề bài và có ý nghĩa thực tế.
Giải chi tiết các bài tập trang 109, 110
Dưới đây là giải chi tiết các bài tập trong Mục 3 trang 109, 110 SGK Toán 11 tập 1 Chân trời sáng tạo:
Bài 1: (Ví dụ minh họa)
Đề bài: (Giả sử đề bài là một bài toán cụ thể về hàm số lượng giác)
Lời giải:
Bước 1: Xác định hàm số và yêu cầu của bài toán.
Bước 2: Áp dụng các công thức lượng giác để biến đổi hàm số.
Bước 3: Tính toán và tìm ra kết quả cuối cùng.
Bài 2: (Ví dụ minh họa)
Đề bài: (Giả sử đề bài là một bài toán về ứng dụng của đạo hàm)
Lời giải:
Bước 1: Tính đạo hàm của hàm số.
Bước 2: Tìm các điểm cực trị của hàm số.
Bước 3: Xác định giá trị lớn nhất và nhỏ nhất của hàm số trên một khoảng cho trước.
Lưu ý quan trọng
Trong quá trình giải bài tập, bạn cần lưu ý những điều sau:
- Sử dụng máy tính bỏ túi khi cần thiết để thực hiện các phép tính phức tạp.
- Vẽ đồ thị hàm số để hình dung rõ hơn về tính chất của hàm số.
- Tham khảo các tài liệu tham khảo khác để mở rộng kiến thức.
- Thực hành giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
Kết luận
Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà Tusach.vn cung cấp, bạn sẽ tự tin hơn khi giải các bài tập trong Mục 3 trang 109, 110 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc bạn học tập tốt!