Quãng đường rơi tự do của một vật được biểu diễn bởi công thức \(s\left( t \right) = 4,9{t^2}\) với \(t\) là thời gian tính bằng giây và \(s\) tính bằng mét.
Vận tốc trung bình của chuyển động này trên khoảng thời gian \(\left[ {5;t} \right]\) hoặc \(\left[ {t;5} \right]\) được tính bằng công thức \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\).
a) Hoàn thiện bảng sau về vận tốc trung bình trong những khoảng thời gian khác nhau. Nêu nhận xét về \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\) khi \(t\) càng gần 5.
b) Giới hạn \(\mathop {\lim }\limits_{t \to 5} \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\) được gọi là vận tốc tức thời của chuyển động tại thời điểm \({t_0} = 5\). Tính giá trị này.
c) Tính giới hạn \(\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}}\) để xác định vận tốc tức thời của chuyển động tại thời điểm \({t_0}\) nào đó trong quá trình rơi của vật.
Phương pháp giải:
a) Thay vào công thức \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\).
b) c) Sử dụng các quy tắc tính giới hạn.
Lời giải chi tiết:
a)
\(\begin{array}{l}\begin{array}{*{20}{l}}{\left[ {5;5,1} \right]}\end{array}:t = 5,1 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{1^2} - 4,{{9.5}^2}}}{{5,1 - 5}} = 49,49\\\begin{array}{*{20}{l}}{\left[ {5;5,05} \right]}\end{array}:t = 5,05 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{05}^2} - 4,{{9.5}^2}}}{{5,05 - 5}} = 49,245\\\begin{array}{*{20}{l}}{\left[ {5;5,01} \right]}\end{array}:t = 5,01 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{01}^2} - 4,{{9.5}^2}}}{{5,01 - 5}} = 49,049\\\begin{array}{*{20}{l}}{\left[ {5;5,001} \right]}\end{array}:t = 5,001 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{001}^2} - 4,{{9.5}^2}}}{{5,001 - 5}} = 49,0049\\\begin{array}{*{20}{l}}{\left[ {4,999;5} \right]}\end{array}:t = 4,999 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{999}^2} - 4,{{9.5}^2}}}{{4,999 - 5}} = 48,9951\\\begin{array}{*{20}{l}}{\left[ {4,99;5} \right]}\end{array}:t = 4,99 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{99}^2} - 4,{{9.5}^2}}}{{4,99 - 5}} = 48,951\end{array}\)
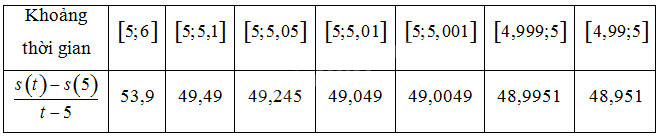
Ta thấy: \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\) càng gần 49 khi \(t\) càng gần 5.
b)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to 5} \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,{{9.5}^2}}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - {5^2}} \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - 5} \right)\left( {t + 5} \right)}}{{t - 5}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + 5} \right) = 4,9\left( {5 + 5} \right) = 49\end{array}\)
c)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,9.t_0^2}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - t_0^2} \right)}}{{t - t_0^2}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - {t_0}} \right)\left( {t + {t_0}} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + {t_0}} \right) = 4,9\left( {{t_0} + {t_0}} \right) = 9,8{t_0}\end{array}\)
