Giải mục 4 trang 68 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 4 trang 68 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn! Tại đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho mục 4 trang 68 sách giáo khoa Toán 11 tập 1 chương trình Chân trời sáng tạo. Bài viết này sẽ giúp bạn hiểu rõ hơn về các khái niệm và phương pháp giải bài tập liên quan.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ quá trình học tập của bạn.
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu ({u_n}) (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ (n).
Hoạt động 5
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu \({u_n}\) (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ \(n\).
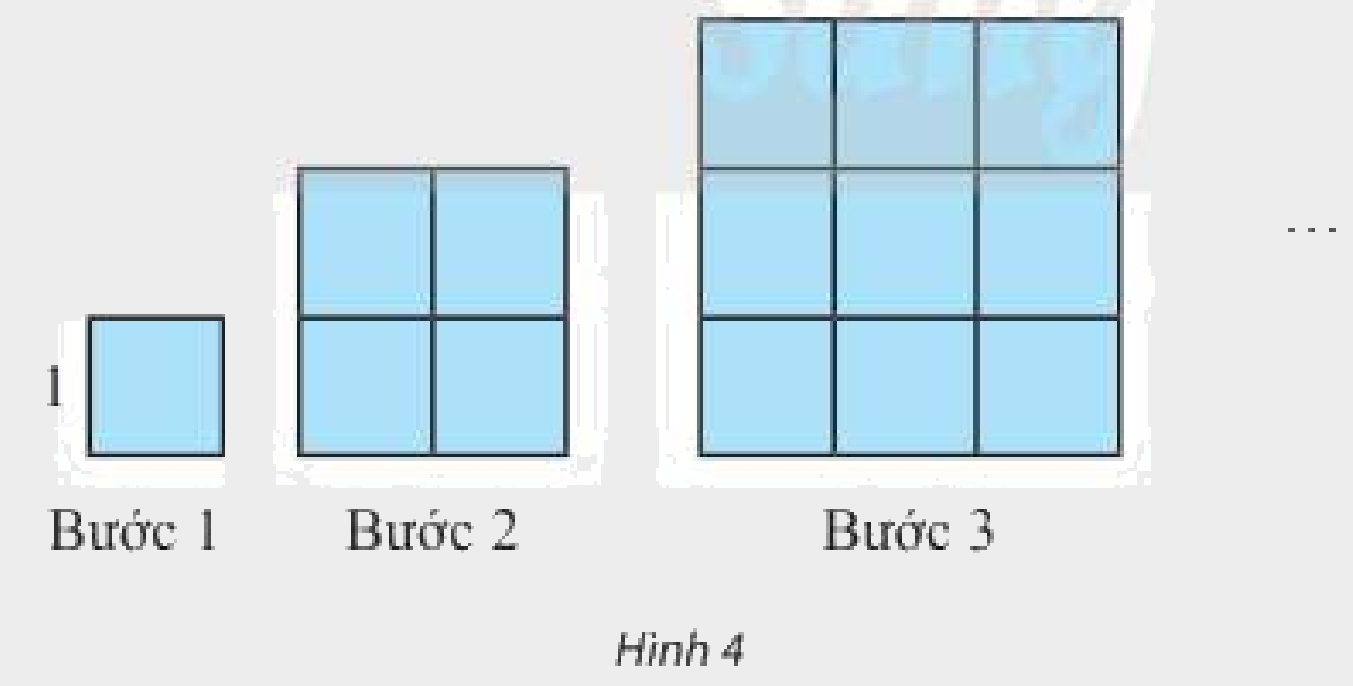
a) Với \(n\) như thế nào thì \({u_n}\) vượt quá 10000; 1000000?
b) Cho hình có diện tích \(S\). Với \(n\) như thế nào thì \({u_n}\) vượt quá \(S\)?
Phương pháp giải:
a) Tìm công thức tổng quát của \({u_n}\) sau đó giải bất phương trình \({u_n} > 10000,{u_n} > 1000000\).
b) Giải bất phương trình \({u_n} > S\).
Lời giải chi tiết:
a) Ta có: \({u_1} = {1^2};{u_2} = {2^2};{u_3} = {3^2};...;{u_n} = {n^2}\)
\(\begin{array}{l}{u_n} > 10000 \Leftrightarrow {n^2} > 10000 = {100^2} \Leftrightarrow n > 100\\{u_n} > 1000000 \Leftrightarrow {n^2} > 1000000 = {1000^2} \Leftrightarrow n > 1000\end{array}\)
b) \({u_n} > S \Leftrightarrow {n^2} > S \Leftrightarrow n > \sqrt S \).
Vậy với các số tự nhiên \(n > \sqrt S \) thì \({u_n} > S\).
Giải mục 4 trang 68 SGK Toán 11 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 4 trang 68 SGK Toán 11 tập 1 Chân trời sáng tạo thường xoay quanh các bài toán về đường thẳng trong không gian, bao gồm việc xác định vị trí tương đối giữa đường thẳng và mặt phẳng, góc giữa đường thẳng và mặt phẳng, và khoảng cách từ một điểm đến đường thẳng hoặc mặt phẳng. Việc nắm vững kiến thức nền tảng về vectơ, phương trình đường thẳng và mặt phẳng là vô cùng quan trọng để giải quyết các bài toán này.
Nội dung chính của mục 4 trang 68
- Kiến thức trọng tâm: Ôn lại các công thức tính góc, khoảng cách, và điều kiện song song, vuông góc giữa đường thẳng và mặt phẳng.
- Các dạng bài tập thường gặp:
- Xác định góc giữa đường thẳng và mặt phẳng.
- Tính khoảng cách từ một điểm đến đường thẳng hoặc mặt phẳng.
- Chứng minh sự song song, vuông góc giữa đường thẳng và mặt phẳng.
- Tìm giao điểm của đường thẳng và mặt phẳng.
Hướng dẫn giải chi tiết các bài tập trong mục 4
Để giải các bài tập trong mục 4 trang 68, bạn cần thực hiện theo các bước sau:
- Đọc kỹ đề bài: Xác định rõ các yếu tố đã cho và yêu cầu của bài toán.
- Vẽ hình: Vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán và các yếu tố liên quan.
- Chọn phương pháp giải: Dựa vào yêu cầu của bài toán, chọn phương pháp giải phù hợp (ví dụ: sử dụng công thức, sử dụng tính chất hình học, sử dụng phương pháp tọa độ).
- Thực hiện giải bài toán: Áp dụng các công thức và tính chất đã học để giải bài toán.
- Kiểm tra lại kết quả: Đảm bảo kết quả của bạn là chính xác và hợp lý.
Ví dụ minh họa: Bài 1 (trang 68 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Lời giải:
- Gọi H là hình chiếu của S lên mặt phẳng (ABCD). Vì SA vuông góc với (ABCD) nên H trùng với A.
- Ta có AC = a√2.
- Trong tam giác SAC vuông tại A, ta có tan(∠SCA) = SA/AC = a/(a√2) = 1/√2.
- Vậy, ∠SCA = arctan(1/√2). Đây chính là góc giữa đường thẳng SC và mặt phẳng (ABCD).
Mẹo giải nhanh và hiệu quả
- Nắm vững các công thức tính góc và khoảng cách.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng hình vẽ minh họa để hiểu rõ hơn về bài toán.
- Kiểm tra lại kết quả sau khi giải xong.
Tài liệu tham khảo thêm
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 11:
- Sách bài tập Toán 11
- Các trang web học Toán trực tuyến
- Các video bài giảng Toán 11 trên YouTube
tusach.vn hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết các bài tập trong mục 4 trang 68 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc bạn học tập tốt!