Giải mục 1 trang 13, 14, 15 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 13, 14, 15 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 13, 14, 15 SGK Toán 11 tập 1, chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài tập và đạt kết quả tốt nhất trong môn Toán.
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác (frac{{2pi
Hoạt động 1
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác \(\frac{{2\pi }}{3}\) và \(\frac{\pi }{4}\) trên
đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy .
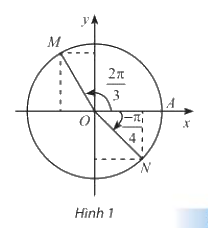
Phương pháp giải:
Dựa vào kiến thức đã học để xác định
Lời giải chi tiết:
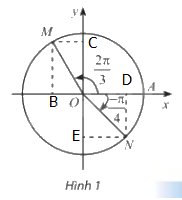
Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy
D,E lần lượt là hình chiếu của N lên Ox, Oy
Ta có OM = ON = 1
\(\widehat {MOC} = \frac{{2\pi }}{3} - \frac{\pi }{2} = \frac{\pi }{6} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {MOC} = \frac{1}{2} = \frac{{MC}}{{OM}} \Rightarrow MC = \frac{1}{2}\\\cos \widehat {MOC} = \frac{{\sqrt 3 }}{2} = \frac{{MB}}{{OM}} \Rightarrow MB = \frac{{\sqrt 3 }}{2}\end{array} \right.\)
Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M \(\left( {\frac{-1}{2};\frac{{\sqrt 3 }}{2}} \right)\)
\(\widehat {NOD} = - \frac{\pi }{4} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {NOD} = - \frac{{\sqrt 2 }}{2} = \frac{{ND}}{{ON}} \Rightarrow ND = - \frac{{\sqrt 2 }}{2}\\\cos \widehat {NOD} = \frac{{\sqrt 2 }}{2} = \frac{{NE}}{{ON}} \Rightarrow NE = \frac{{\sqrt 2 }}{2}\end{array} \right.\)
Tọa độ của điểm N \(\left( { \frac{{\sqrt 2 }}{2};\frac{-{\sqrt 2 }}{2}} \right)\)
Thực hành
Tính \(\sin \left( { - \frac{{2\pi }}{3}} \right)\) và \(\tan 495^\circ \)
Phương pháp giải:
Dựa vào kiến thức đã học ở phần trên để tính
Lời giải chi tiết:
\(\begin{array}{l}\sin \left( { - \frac{{2\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2}\\\tan 495^\circ = - 1\end{array}\)
Giải mục 1 trang 13, 14, 15 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 1 của chương trình Toán 11 tập 1, Chân trời sáng tạo, tập trung vào việc giới thiệu về hàm số và đồ thị hàm số. Đây là một trong những chủ đề quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn. Việc nắm vững các khái niệm, định nghĩa và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Nội dung chính của Mục 1
- Khái niệm hàm số: Định nghĩa hàm số, tập xác định, tập giá trị.
- Các loại hàm số thường gặp: Hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit.
- Đồ thị hàm số: Cách vẽ đồ thị hàm số, các tính chất của đồ thị.
- Ứng dụng của hàm số: Giải các bài toán thực tế liên quan đến hàm số.
Giải chi tiết các bài tập trang 13, 14, 15
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1, trang 13, 14, 15 SGK Toán 11 tập 1 - Chân trời sáng tạo:
Bài 1 (Trang 13)
Đề bài: (Ví dụ về đề bài)
Lời giải: (Giải thích chi tiết từng bước, kèm theo công thức và ví dụ minh họa)
Bài 2 (Trang 14)
Đề bài: (Ví dụ về đề bài)
Lời giải: (Giải thích chi tiết từng bước, kèm theo công thức và ví dụ minh họa)
Bài 3 (Trang 15)
Đề bài: (Ví dụ về đề bài)
Lời giải: (Giải thích chi tiết từng bước, kèm theo công thức và ví dụ minh họa)
Mẹo giải bài tập hàm số hiệu quả
- Nắm vững định nghĩa và tính chất của hàm số: Đây là nền tảng để giải quyết mọi bài tập.
- Sử dụng các công thức và phương pháp giải phù hợp: Tùy thuộc vào từng loại hàm số và bài tập cụ thể.
- Vẽ đồ thị hàm số: Giúp hình dung rõ hơn về tính chất của hàm số và tìm ra nghiệm của phương trình.
- Kiểm tra lại kết quả: Đảm bảo tính chính xác của lời giải.
Tài liệu tham khảo hữu ích
Ngoài SGK, các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 11:
- Sách bài tập Toán 11
- Các trang web học Toán trực tuyến
- Video bài giảng Toán 11
Tusach.vn hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc học tập và giải bài tập Toán 11. Chúc các em học tốt!
| Bài tập | Trang | Độ khó |
|---|---|---|
| Bài 1 | 13 | Dễ |
| Bài 2 | 14 | Trung bình |
| Bài 3 | 15 | Khó |
| Nguồn: tusach.vn | ||