Bài 8 trang 82 SGK Toán 11 tập 2 – Chân trời sáng tạo
Tổng quan nội dung
Bài 8 trang 82 SGK Toán 11 Tập 2 – Chân trời sáng tạo
Bài 8 trang 82 SGK Toán 11 Tập 2 thuộc chương trình Toán 11, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, các phép biến đổi lượng giác và giải phương trình lượng giác để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Tính thể tích của khối chóp cụt lục giác đều (ABCDEF.{rm{ }}A'B'C'D'E'F') với (O) và (O') là tâm hai đáy
Đề bài
Tính thể tích của khối chóp cụt lục giác đều \(ABCDEF.{\rm{ }}A'B'C'D'E'F'\) với \(O\) và \(O'\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\frac{a}{2},OO' = a\).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).
Lời giải chi tiết
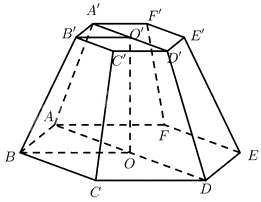
Diện tích đáy lớn là: \(S = 6{S_{ABO}} = 6.\frac{{A{B^2}\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{2}\)
Diện tích đáy bé là: \(S' = 6{S_{A'B'O'}} = 6.\frac{{A'B{'^2}\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{8}\)
Thể tích khối chóp cụt lục giác đều là:
\(V = \frac{1}{3}.a\left( {\frac{{3{a^2}\sqrt 3 }}{2} + \sqrt {\frac{{3{a^2}\sqrt 3 }}{2}.\frac{{3{a^2}\sqrt 3 }}{8}} + \frac{{3{a^2}\sqrt 3 }}{8}} \right) = \frac{{3{a^3}\sqrt 3 }}{8}\)
Bài 8 trang 82 SGK Toán 11 Tập 2 – Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 8 trang 82 SGK Toán 11 Tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về hàm số lượng giác và các ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 8 yêu cầu giải các phương trình lượng giác sau:
- sin(x + π/3) = sin(x - π/4)
- cos(2x) = cos(x + π/3)
- tan(x) = tan(π/5)
- cot(x) = cot(2x)
Lời giải chi tiết
1. Giải phương trình sin(x + π/3) = sin(x - π/4)
Sử dụng công thức sin(a) = sin(b) ⇔ a = b + k2π hoặc a = π - b + k2π (k ∈ Z).
- Trường hợp 1: x + π/3 = x - π/4 + k2π ⇔ π/3 + π/4 = k2π ⇔ 7π/12 = k2π ⇔ k = 7/24 (không phải số nguyên, loại)
- Trường hợp 2: x + π/3 = π - (x - π/4) + k2π ⇔ x + π/3 = π - x + π/4 + k2π ⇔ 2x = π - π/3 - π/4 + k2π ⇔ 2x = 5π/12 + k2π ⇔ x = 5π/24 + kπ (k ∈ Z)
Vậy nghiệm của phương trình là x = 5π/24 + kπ (k ∈ Z).
2. Giải phương trình cos(2x) = cos(x + π/3)
Sử dụng công thức cos(a) = cos(b) ⇔ a = b + k2π hoặc a = -b + k2π (k ∈ Z).
- Trường hợp 1: 2x = x + π/3 + k2π ⇔ x = π/3 + k2π (k ∈ Z)
- Trường hợp 2: 2x = -x - π/3 + k2π ⇔ 3x = -π/3 + k2π ⇔ x = -π/9 + k2π/3 (k ∈ Z)
Vậy nghiệm của phương trình là x = π/3 + k2π và x = -π/9 + k2π/3 (k ∈ Z).
3. Giải phương trình tan(x) = tan(π/5)
Sử dụng công thức tan(a) = tan(b) ⇔ a = b + kπ (k ∈ Z).
Vậy nghiệm của phương trình là x = π/5 + kπ (k ∈ Z).
4. Giải phương trình cot(x) = cot(2x)
Sử dụng công thức cot(a) = cot(b) ⇔ a = b + kπ (k ∈ Z).
Vậy nghiệm của phương trình là x = 2x + kπ ⇔ -x = kπ ⇔ x = -kπ (k ∈ Z). Tuy nhiên, cần lưu ý điều kiện xác định của cot(x) và cot(2x). x ≠ kπ và 2x ≠ kπ (tức x ≠ kπ/2). Do đó, nghiệm x = -kπ không thỏa mãn điều kiện xác định. Vậy phương trình vô nghiệm.
Lưu ý khi giải bài tập
- Luôn kiểm tra điều kiện xác định của hàm số lượng giác.
- Sử dụng đúng các công thức lượng giác.
- Biết cách biến đổi phương trình lượng giác về dạng cơ bản.
Hy vọng lời giải chi tiết này sẽ giúp các bạn hiểu rõ hơn về Bài 8 trang 82 SGK Toán 11 Tập 2 – Chân trời sáng tạo. Chúc các bạn học tốt!