Bài 8 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 8 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài 8 trang 24 SGK Toán 11 Tập 1 thuộc chương trình học Toán 11, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về các loại hàm số, tính đơn điệu, cực trị và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
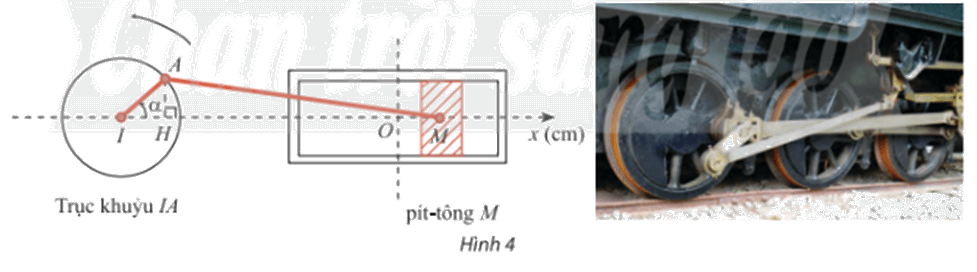
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA.
Đề bài
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho \(\alpha \) là góc quay của trục khuỷu, O là vị trí của pít – tông khi \(\alpha = \frac{\pi }{2}\) và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.
a) Biết IA = 8cm, viết công thức tính tọa độ \({x_M}\) của điểm M trên trục Ox theo \(\alpha \).
b) Ban đầu \(\alpha = 0\). Sau 1 phút chuyển động, \({x_M}\)= – 3cm. Xác định \({x_M}\) sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười.
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ.
Lời giải chi tiết
a) Tại \(\alpha = \frac{\pi }{2}\) thì H trùng I, M trùng O nên MH = OI do đó OM = IH.
Xét tam giác AHI vuông tại H có: \(IH = cos\alpha .IA = 8cos\alpha .\)
\( \Rightarrow {x_M} = OM = IH = 8cos\alpha \).
b) Giả sử sau khi chuyển động được 1 phút, trục khuỷu quay được một góc là \(\alpha \).
Khi đó \({x_M} = - 3cm \Rightarrow cos\alpha = - \frac{3}{8}\).
Sau khi chuyển động 2 phút, trục khuỷu quay được một góc \(2\alpha \), nên:
\({x_M} = 8cos2\alpha = 8\left( {2{{\cos }^2}\alpha - 1} \right)\)\( = 8\left( {2{{\left( { - \frac{3}{8}} \right)}^2} - 1} \right) \approx - 5,8 cm\).
Bài 8 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 8 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số và ứng dụng của đạo hàm. Dưới đây là giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 8 yêu cầu học sinh giải các bài toán liên quan đến việc xác định tính đơn điệu của hàm số, tìm cực trị và vẽ đồ thị hàm số. Cụ thể, bài tập có thể bao gồm:
- Xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm điểm cực đại, cực tiểu của hàm số.
- Vẽ đồ thị hàm số dựa trên các thông tin đã tìm được.
Hướng dẫn giải chi tiết
Để giải bài 8 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo, học sinh cần nắm vững các kiến thức sau:
- Đạo hàm: Hiểu rõ khái niệm đạo hàm, quy tắc tính đạo hàm của các hàm số cơ bản và các phép toán trên đạo hàm.
- Tính đơn điệu của hàm số: Biết cách sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số.
- Cực trị của hàm số: Nắm vững điều kiện để hàm số có cực đại, cực tiểu và cách tìm tọa độ các điểm cực trị.
- Đồ thị hàm số: Biết cách vẽ đồ thị hàm số dựa trên các thông tin về khoảng đồng biến, nghịch biến, cực trị và giao điểm với các trục tọa độ.
Ví dụ minh họa:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Để xác định khoảng đồng biến, nghịch biến của hàm số, ta tính đạo hàm f'(x) = 3x2 - 6x. Sau đó, ta giải phương trình f'(x) = 0 để tìm các điểm cực trị. Từ đó, ta có thể xác định khoảng đồng biến, nghịch biến của hàm số.
Lưu ý khi giải bài tập
Khi giải bài 8 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo, học sinh cần lưu ý những điều sau:
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài tập.
- Sử dụng đúng các công thức và quy tắc đạo hàm.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
- Rèn luyện kỹ năng vẽ đồ thị hàm số.
Tài liệu tham khảo
Ngoài SGK Toán 11 Tập 1 - Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
- Sách bài tập Toán 11.
- Các trang web học toán trực tuyến như tusach.vn.
- Các video bài giảng trên YouTube.
Kết luận
Bài 8 trang 24 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và ứng dụng của đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và rèn luyện kỹ năng giải toán, học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.
| Hàm số | Đạo hàm | Khoảng đồng biến | Khoảng nghịch biến |
|---|---|---|---|
| f(x) = x3 - 3x2 + 2 | f'(x) = 3x2 - 6x | (-∞; 0) và (2; +∞) | (0; 2) |